Coding Schemes

2017-06-23 3 min read rstats 
library(tidyverse)
library(lmerTest)

How you choose to code categorical variables changes how you can interpret the intercept and effects of those variables. My favourite tutorial on coding schemes explains things in detail. I’m just adding some concrete examples below.

First, I simulated a data frame of 100 raters rating 100 faces each. Female faces get ratings with a mean of 6; male faces get ratings with a mean of 5 (I know, ratings are usually ordinal integers, but let’s pretend we used something like a slider). To simulate random effects, both raters and faces have random intercepts with SDs of 1.

set.seed(555)  # for reproducibility; delete when running simulations

n_raters <- 100
n_faces <- 100

female_mean <- 6
male_mean <- 5

raters <- tibble(
  rater_id = 1:n_raters,
  rater_i = rnorm(n_raters)
)

faces <- tibble(
  face_id = 1:n_faces,
  face_i = rnorm(n_faces),
  face_sex = rep(c("female", "male"), each = n_faces/2)
)

df <- expand.grid(
  face_id = faces$face_id,
  rater_id = raters$rater_id
) %>%
  left_join(faces, by = "face_id") %>%
  left_join(raters, by = "rater_id") %>%
  mutate(
    face_sex_i = ifelse(face_sex=="male", male_mean, female_mean),
    error = rnorm(nrow(.)),
    rating = face_i + rater_i + face_sex_i + error
  )

Calculate the means and SDs of the female and male faces.

face_sex mean SD
female 5.940 1.767
male 5.114 1.649

Always graph your data to confirm you simulated it correctly.

df %>% 
  ggplot(aes(face_sex, rating)) + 
  geom_violin() +
  geom_boxplot(width=0.2)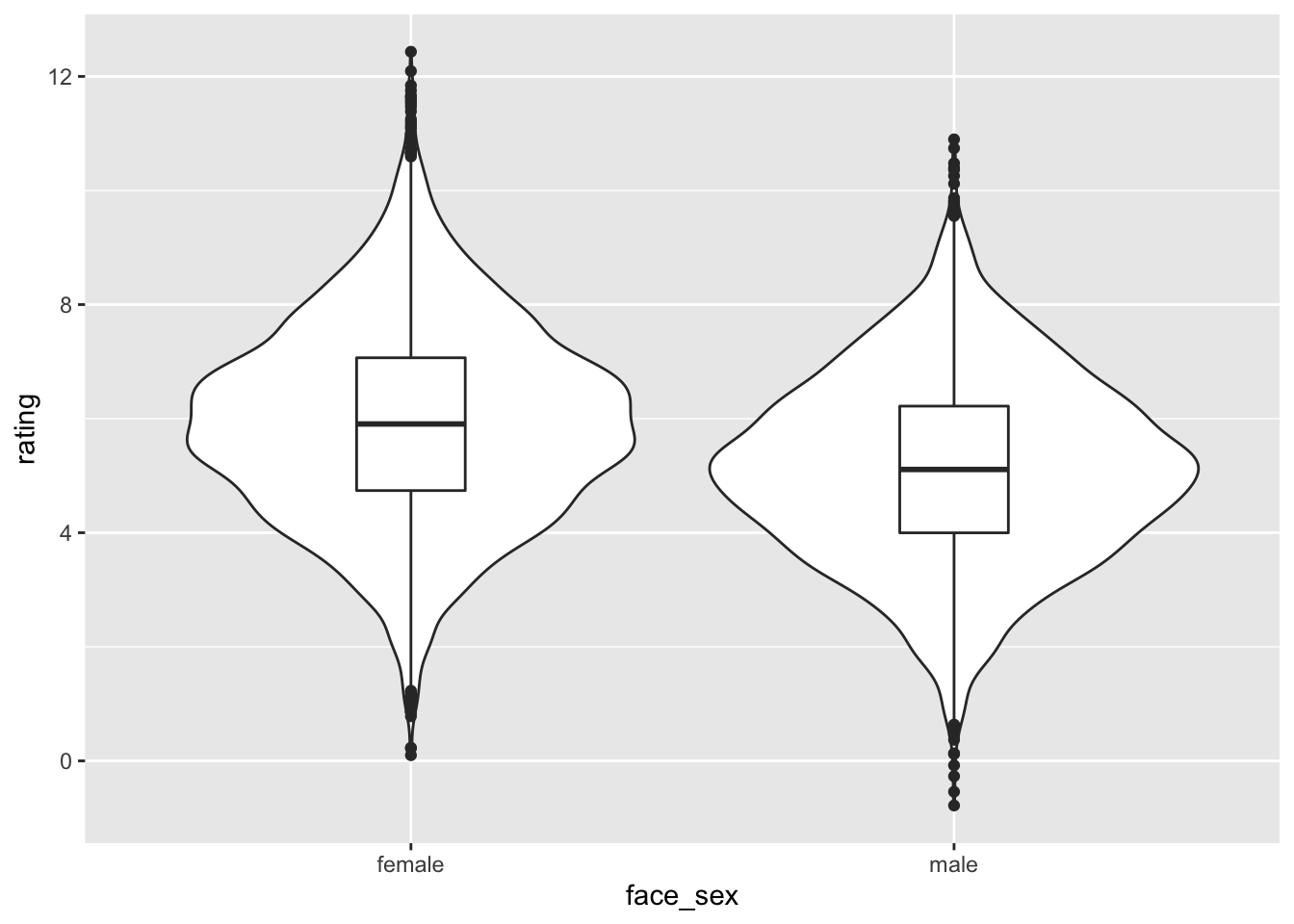

Recode face sex using treatment, sum, or effect coding.

df2 <- df %>%
  mutate(
    face_sex.tr = recode(face_sex, "female" = 1, "male" = 0),
    face_sex.sum = recode(face_sex, "female" = -1, "male" = 1),
    face_sex.e = recode(face_sex, "female" = -0.5, "male" = 0.5)
  )

Now we analyse the data using each of the 4 styles of coding. I’m just going to show the table of fixed effects.

Categorical coding

m1 <- lmerTest::lmer(rating ~ face_sex + 
                       (1 | face_id) + 
                       (1 + face_sex | rater_id), 
                     data = df2)
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 5.940 0.174 173.360 34.080 0
face_sexmale -0.826 0.203 98.586 -4.069 0

Note that the intercept coefficient is equal to the female mean (5.94) and the effect of face sex is how much less the male mean is (5.114 - 5.94 = -0.826).

Treatment coding

m.tr <- lmerTest::lmer(rating ~ face_sex.tr + 
               (1 | face_id) + 
               (1 + face_sex.tr | rater_id), 
             data = df2)
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 5.114 0.172 169.515 29.720 0
face_sex.tr 0.826 0.203 98.611 4.069 0

Treatment coding is the same as categorical coding, but gives you more control over what the reference category is. Here, the reference category is male and the “treatment” category is female, so the intercept coefficient is equal to the male mean (5.114) and the effect of face sex is how much more the female mean is (5.94 - 5.114 = 0.826).

Sum coding

m.sum <- lmerTest::lmer(rating ~ face_sex.sum + 
                (1 | face_id) + 
                (1 + face_sex.sum | rater_id), 
              data = df2)
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 5.527 0.140 194.675 39.387 0
face_sex.sum -0.413 0.102 98.601 -4.069 0

With sum coding, the intercept coefficient is equal to the overall mean ignoring face sex (i.e., (5.94 + 5.114)/2 = 5.527) and the effect of face sex is how much above and below that each of the two face sexes differ from the mean (i.e., (5.94 - 5.114)/2 = 0.413).

Effect coding

m.e <- lmerTest::lmer(rating ~ face_sex.e + 
              (1 | face_id) + 
              (1 + face_sex.e | rater_id), 
            data = df2)
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 5.527 0.140 194.683 39.387 0
face_sex.e -0.826 0.203 98.604 -4.069 0

With effect coding, the intercept coefficient is the same as sum coding and the effect of face sex is how much the two face sexes differ from each other (i.e., 5.94 - 5.114 = 0.826). Note that this coefficient is double that from the sum coding.

R coding effect treatment lmer mixed effects simulation
Lisa DeBruine
Lisa DeBruine
Professor of Psychology

Lisa DeBruine is a professor of psychology at the University of Glasgow. Her substantive research is on the social perception of faces and kinship. Her meta-science interests include team science (especially the Psychological Science Accelerator), open documentation, data simulation, web-based tools for data collection and stimulus generation, and teaching computational reproducibility.

Related