Mixed Effects

Lisa DeBruine

Generate data for a Stroop task where people (subjects) say the colour of colour words (stimuli) shown in each of two versions (congruent and incongruent). Subjects are in one of two conditions (hard or easy). The dependent variable (DV) is reaction time.

We expect people to have faster reaction times for congruent stimuli than incongruent stimuli (main effect of version) and to be faster in the easy condition than the hard condition (main effect of condition). We’ll look at some different interaction patterns below.

Setup

library(tidyverse)   # for data wrangling, pipes, and good dataviz
library(afex)        # for mixed effect models
library(broom.mixed) # for getting tidy data tables from mixed models
library(faux)        # for simulating correlated variables

options(digits = 4, scipen = 10)

Simulation

Random Factors

First, set up the overall structure of your data by specifying the number of observations for each random factor. Here, we have a crossed design, so each subject responds to each stimulus. We’ll set the numbers to small numbers as a demo first.

sub_n  <- 2 # number of subjects in this simulation
stim_n  <- 2 # number of stimuli in this simulation

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n)

dat
## # A tibble: 4 × 2
##   sub   stim 
##   <chr> <chr>
## 1 sub1  stim1
## 2 sub1  stim2
## 3 sub2  stim1
## 4 sub2  stim2

Fixed Factors

Next, add the fixed factors. Specify if they vary between one of the random factors and specify the names of the levels.

Each subject is in only one condition, so the code below assigns half easy and half hard. You can change the proportion of subjects assigned each level with the .prob argument.

Stimuli are seen in both congruent and incongruent versions, so this will double the number of rows in our resulting data set.

sub_n  <- 2 # number of subjects in this simulation
stim_n  <- 2 # number of stimuli in this simulation

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n) |>
  add_between(.by = "sub", condition = c("easy","hard")) |>
  add_within(version = c("congruent", "incongruent"))

dat
## # A tibble: 8 × 4
##   sub   stim  condition version    
##   <chr> <chr> <fct>     <fct>      
## 1 sub1  stim1 easy      congruent  
## 2 sub1  stim1 easy      incongruent
## 3 sub1  stim2 easy      congruent  
## 4 sub1  stim2 easy      incongruent
## 5 sub2  stim1 hard      congruent  
## 6 sub2  stim1 hard      incongruent
## 7 sub2  stim2 hard      congruent  
## 8 sub2  stim2 hard      incongruent

Contrast Coding

To be able to calculate the dependent variable, you need to recode categorical variables into numbers. Use the helper function add_contrast() for this. The code below creates anova-coded versions of condition and version. Luckily for us, the factor levels default to a sensible order, with “easy” predicted to have a faster (lower) reactive time than “hard”, and “congruent” predicted to have a faster RT than “incongruent”, but we can also customise the order of levels with add_contrast(); see the contrasts vignette for more details.

sub_n  <- 2 # number of subjects in this simulation
stim_n  <- 2 # number of stimuli in this simulation

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n) |>
  add_between(.by = "sub", condition = c("easy","hard")) |>
  add_within(version = c("congruent", "incongruent")) |>
  add_contrast("condition") |>
  add_contrast("version")

dat
## # A tibble: 8 × 6
##   sub   stim  condition version     `condition.hard-easy` version.incongruent-…¹
##   <chr> <chr> <fct>     <fct>                       <dbl>                  <dbl>
## 1 sub1  stim1 easy      congruent                    -0.5                   -0.5
## 2 sub1  stim1 easy      incongruent                  -0.5                    0.5
## 3 sub1  stim2 easy      congruent                    -0.5                   -0.5
## 4 sub1  stim2 easy      incongruent                  -0.5                    0.5
## 5 sub2  stim1 hard      congruent                     0.5                   -0.5
## 6 sub2  stim1 hard      incongruent                   0.5                    0.5
## 7 sub2  stim2 hard      congruent                     0.5                   -0.5
## 8 sub2  stim2 hard      incongruent                   0.5                    0.5
## # ℹ abbreviated name: ¹​`version.incongruent-congruent`

The function defaults to very descriptive names that help you interpret the fixed factors. Here, “condition.hard-easy” means the main effect of this factor is interpreted as the RT for hard trials minus the RT for easy trials, and “version.incongruent-congruent” means the main effect of this factor is interpreted as the RT for incongruent trials minus the RT for congruent trials. However, we can change these to simpler labels with the colnames argument.

Random Effects

Now we specify the random effect structure. We’ll just add random intercepts to start, but will conver random slopes later.

Each subject will have slightly faster or slower reaction times on average; this is their random intercept (sub_i). We’ll model it from a normal distribution with a mean of 0 and SD of 100ms.

Each stimulus will have slightly faster or slower reaction times on average; this is their random intercept (stim_i). We’ll model it from a normal distribution with a mean of 0 and SD of 50ms (it seems reasonable to expect less variability between words than people for this task).

Run this code a few times to see how the random effects change each time. this is because they are sampled from populations.

sub_n  <- 2 # number of subjects in this simulation
stim_n  <- 2 # number of stimuli in this simulation
sub_sd <- 100 # SD for the subjects' random intercept
stim_sd <- 50 # SD for the stimuli's random intercept

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n) |>
  add_between(.by = "sub", condition = c("easy","hard")) |>
  add_within(version = c("congruent", "incongruent")) |>
  add_contrast("condition", colnames = "cond") |>
  add_contrast("version", colnames = "vers") |>
  add_ranef(.by = "sub", sub_i = sub_sd) |>
  add_ranef(.by = "stim", stim_i = stim_sd)

dat
## # A tibble: 8 × 8
##   sub   stim  condition version      cond  vers sub_i stim_i
##   <chr> <chr> <fct>     <fct>       <dbl> <dbl> <dbl>  <dbl>
## 1 sub1  stim1 easy      congruent    -0.5  -0.5 -99.7  -30.9
## 2 sub1  stim1 easy      incongruent  -0.5   0.5 -99.7  -30.9
## 3 sub1  stim2 easy      congruent    -0.5  -0.5 -99.7  101. 
## 4 sub1  stim2 easy      incongruent  -0.5   0.5 -99.7  101. 
## 5 sub2  stim1 hard      congruent     0.5  -0.5  72.2  -30.9
## 6 sub2  stim1 hard      incongruent   0.5   0.5  72.2  -30.9
## 7 sub2  stim2 hard      congruent     0.5  -0.5  72.2  101. 
## 8 sub2  stim2 hard      incongruent   0.5   0.5  72.2  101.

Error Term

Finally, add an error term. This uses the same add_ranef() function, just without specifying which random factor it’s for with .by. In essence, this samples an error value from a normal distribution with a mean of 0 and the specified SD for each trial. We’ll also increase the number of subjects and stimuli to more realistic values now.

sub_n    <- 200 # number of subjects in this simulation
stim_n   <- 50  # number of stimuli in this simulation
sub_sd   <- 100 # SD for the subjects' random intercept
stim_sd  <- 50  # SD for the stimuli's random intercept
error_sd <- 25  # residual (error) SD

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n) |>
  add_between(.by = "sub", condition = c("easy","hard")) |>
  add_within(version = c("congruent", "incongruent")) |>
  add_contrast("condition", colnames = "cond") |>
  add_contrast("version", colnames = "vers") |>
  add_ranef(.by = "sub", sub_i = sub_sd) |>
  add_ranef(.by = "stim", stim_i = stim_sd) |>
  add_ranef(err = error_sd)

Calculate DV

Now we can calculate the DV by adding together an overall intercept (mean RT for all trials), the subject-specific intercept, the stimulus-specific intercept, and an error term, plus the effect of subject condition, the effect of stimulus version, and the interaction between condition and version.

We set these effects in raw units (ms). So when we set the effect of subject condition (sub_cond_eff) to 50, that means the average difference between the easy and hard condition is 50ms. Easy was coded as -0.5 and hard was coded as +0.5, which means that trials in the easy condition have -0.5 * 50ms (i.e., -25ms) added to their reaction time, while trials in the hard condition have +0.5 * 50ms (i.e., +25ms) added to their reaction time.

sub_n         <- 200 # number of subjects in this simulation
stim_n        <- 50  # number of stimuli in this simulation
sub_sd        <- 100 # SD for the subjects' random intercept
stim_sd       <- 50  # SD for the stimuli's random intercept
error_sd      <- 25  # residual (error) SD
grand_i       <- 400 # overall mean DV
cond_eff      <- 50  # mean difference between conditions: hard - easy
vers_eff      <- 50  # mean difference between versions: incongruent - congruent
cond_vers_ixn <-  0  # interaction between version and condition

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n) |>
  add_between(.by = "sub", condition = c("easy","hard")) |>
  add_within(version = c("congruent", "incongruent")) |>
  add_contrast("condition", colnames = "cond") |>
  add_contrast("version", colnames = "vers") |>
  add_ranef(.by = "sub", sub_i = sub_sd) |>
  add_ranef(.by = "stim", stim_i = stim_sd) |>
  add_ranef(err = error_sd) |>
  mutate(dv = grand_i + sub_i + stim_i + err +
         (cond * cond_eff) + 
         (vers * vers_eff) + 
         (cond * vers * cond_vers_ixn) # in this example, this is always 0 and could be omitted
  )

As always, graph to make sure you’ve simulated the general pattern you expected.

ggplot(dat, aes(condition, dv, color = version)) +
  geom_hline(yintercept = grand_i) +
  geom_violin(alpha = 0.5) +
  stat_summary(fun = mean,
               fun.min = \(x){mean(x) - sd(x)},
               fun.max = \(x){mean(x) + sd(x)},
               position = position_dodge(width = 0.9)) +
  scale_color_brewer(palette = "Dark2")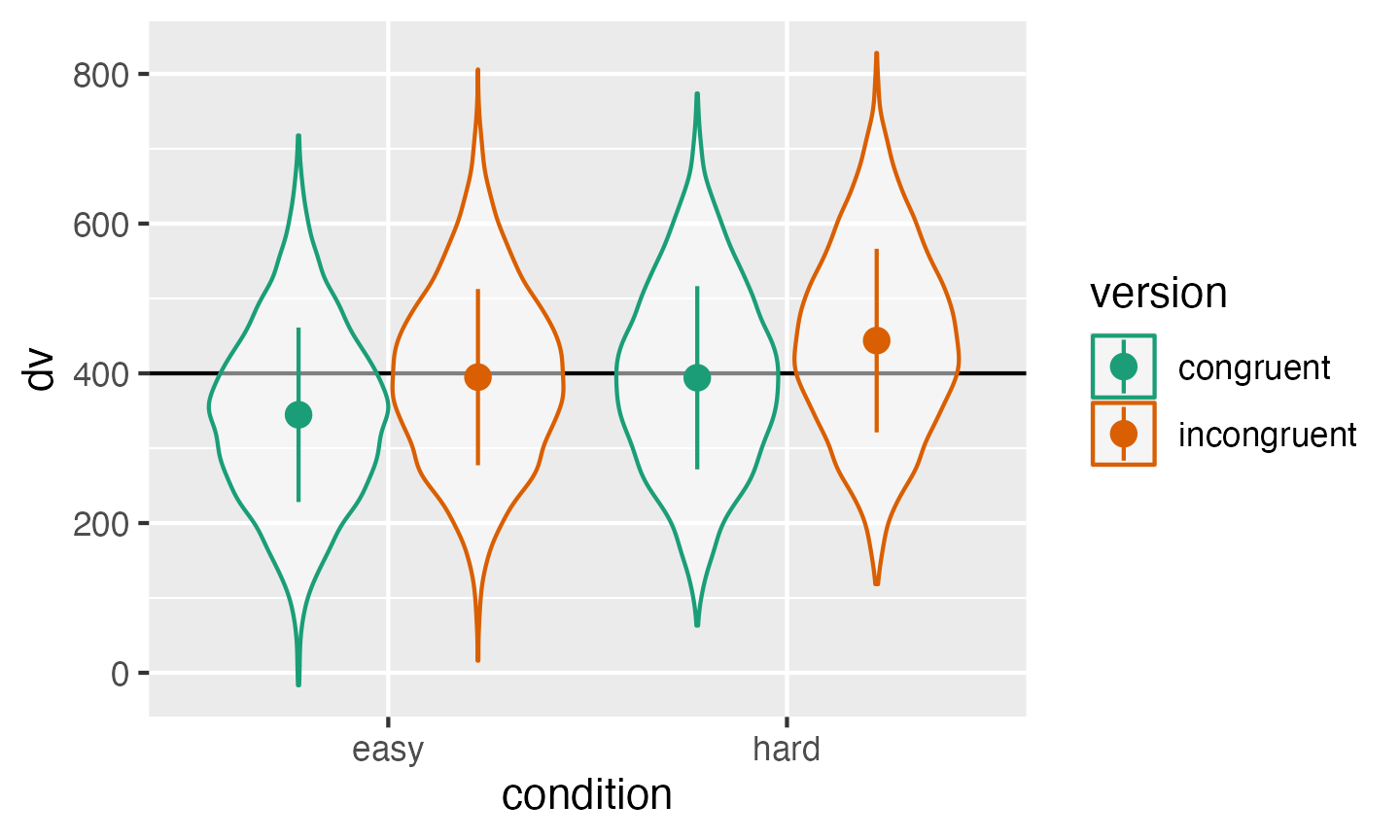

Double-check the simulated pattern

Interactions

If you want to simulate an interaction, it can be tricky to figure out what to set the main effects and interaction effect to. It can be easier to think about the simple main effects for each cell. Create four new variables and set them to the deviations from the overall mean you’d expect for each condition (so they should add up to 0). Here, we’re simulating a small effect of version in the hard condition (50ms difference) and double that effect of version in the easy condition (100ms difference).

# set variables to use in calculations below
hard_congr <- -25
hard_incon <- +25
easy_congr <- -50
easy_incon <- +50

Use the code below to transform the simple main effects above into main effects and interactions for use in the equations below.

# calculate main effects and interactions from simple effects above

# mean difference between easy and hard conditions
cond_eff     <- (hard_congr + hard_incon)/2 -
                (easy_congr + easy_incon)/2

# mean difference between incongruent and congruent versions
vers_eff <- (hard_incon + easy_incon)/2 - 
            (hard_congr + easy_congr)/2

# interaction between version and condition
cond_vers_ixn <- (hard_incon - hard_congr) -
                 (easy_incon - easy_congr)

Then generate the DV the same way we did above, but also add the interaction effect multiplied by the effect-coded subject condition and stimulus version.

dat <- add_random(sub = sub_n) |>
  add_random(stim = stim_n) |>
  add_between(.by = "sub", condition = c("easy","hard")) |>
  add_within(version = c("congruent", "incongruent")) |>
  add_contrast("condition", colnames = "cond") |>
  add_contrast("version", colnames = "vers") |>
  add_ranef(.by = "sub", sub_i = sub_sd) |>
  add_ranef(.by = "stim", stim_i = stim_sd) |>
  add_ranef(err = error_sd) |>
  mutate(dv = grand_i + sub_i + stim_i + err +
         (cond * cond_eff) + 
         (vers * vers_eff) + 
         (cond * vers * cond_vers_ixn)
  )

ggplot(dat, aes(condition, dv, color = version)) +
  geom_hline(yintercept = grand_i) +
  geom_violin(alpha = 0.5) +
  stat_summary(fun = mean,
               fun.min = \(x){mean(x) - sd(x)},
               fun.max = \(x){mean(x) + sd(x)},
               position = position_dodge(width = 0.9)) +
  scale_color_brewer(palette = "Dark2")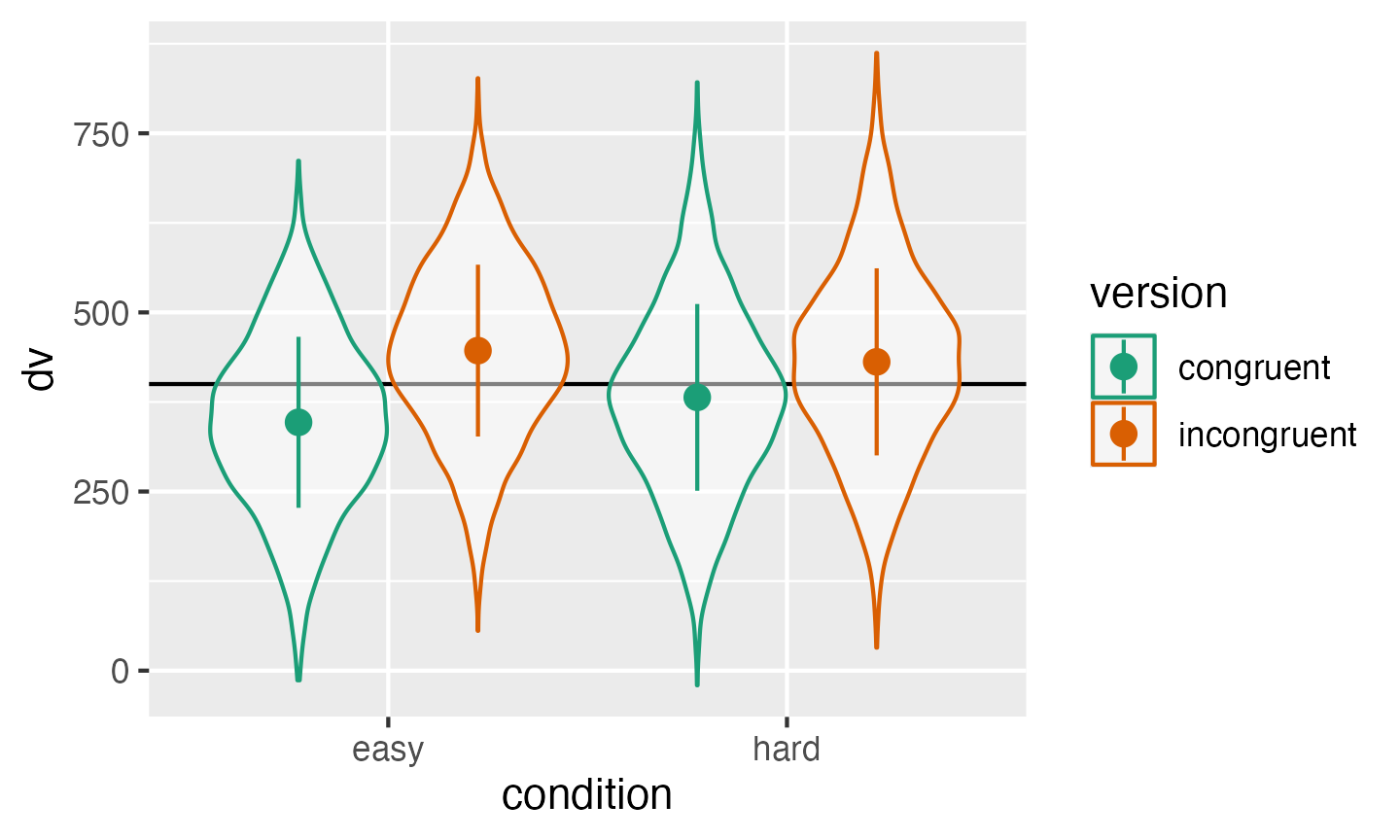

Double-check the interaction between condition and version

group_by(dat, condition, version) %>%
  summarise(m = mean(dv) - grand_i %>% round(1),
            .groups = "drop") %>%
  pivot_wider(names_from = version, 
              values_from = m)
## # A tibble: 2 × 3
##   condition congruent incongruent
##   <fct>         <dbl>       <dbl>
## 1 easy          -53.4        46.7
## 2 hard          -18.6        31.0

Analysis

New we will run a linear mixed effects model with lmer and look at the summary.

mod <- lmer(dv ~ cond * vers +
              (1 | sub) + 
              (1 | stim),
            data = dat)

mod.sum <- summary(mod)

mod.sum
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: dv ~ cond * vers + (1 | sub) + (1 | stim)
##    Data: dat
## 
## REML criterion at convergence: 187474
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -4.154 -0.668  0.000  0.674  4.604 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sub      (Intercept) 12456    111.6   
##  stim     (Intercept)  2755     52.5   
##  Residual               628     25.1   
## Number of obs: 20000, groups:  sub, 200; stim, 50
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)   401.417     10.835   168.868   37.05   <2e-16 ***
## cond            9.554     15.788   198.000    0.61     0.55    
## vers           74.834      0.354 19749.000  211.16   <2e-16 ***
## cond:vers     -50.516      0.709 19749.000  -71.27   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) cond  vers 
## cond      0.000             
## vers      0.000  0.000      
## cond:vers 0.000  0.000 0.000

Sense checks

First, check that your groups make sense.

• The number of obs should be the total number of trials analysed.
• sub should be what we set sub_n to above.
• stim should be what we set stim_n to above.

mod.sum$ngrps |>
  as_tibble(rownames = "Random.Fator") |>
  mutate(parameters = c(sub_n, stim_n))
## # A tibble: 2 × 3
##   Random.Fator value parameters
##   <chr>        <dbl>      <dbl>
## 1 sub            200        200
## 2 stim            50         50

Next, look at the random effects.

• The SD for sub should be near sub_sd.
• The SD for stim should be near stim_sd.
• The residual SD should be near error_sd.

mod.sum$varcor |>
  as_tibble() |>
  select(Groups = grp, Name = var1, "Std.Dev." = sdcor) |>
  mutate(parameters = c(sub_sd, stim_sd, error_sd))
## # A tibble: 3 × 4
##   Groups   Name        Std.Dev. parameters
##   <chr>    <chr>          <dbl>      <dbl>
## 1 sub      (Intercept)    112.         100
## 2 stim     (Intercept)     52.5         50
## 3 Residual NA              25.1         25

Finally, look at the fixed effects.

• The estimate for the Intercept should be near the grand_i.
• The main effect of cond should be near what we calculated for cond_eff.
• The main effect of vers should be near what we calculated for vers_eff.
• The interaction between cond:vers should be near what we calculated for cond_vers_ixn.

mod.sum$coefficients |>
  as_tibble(rownames = "Effect") |>
  select(Effect, Estimate) |>
  mutate(parameters = c(grand_i, cond_eff, vers_eff, cond_vers_ixn))
## # A tibble: 4 × 3
##   Effect      Estimate parameters
##   <chr>          <dbl>      <dbl>
## 1 (Intercept)   401.          400
## 2 cond            9.55          0
## 3 vers           74.8          75
## 4 cond:vers     -50.5         -50

Random effects

Plot the subject intercepts from our code above (dat$sub_i) against the subject intercepts calculated by lmer (ranef(mod)$sub_id).

# get simulated random intercept for each subject
sub_sim <- dat |>
  group_by(sub, sub_i) |>
  summarise(.groups = "drop")

# join to calculated random intercept from model
sub_sim_mod <- ranef(mod)$sub |>
  as_tibble(rownames = "sub") |>
  rename(mod_sub_i = `(Intercept)`) |>
  left_join(sub_sim, by = "sub")

# plot to check correspondence
sub_sim_mod |>
  ggplot(aes(sub_i,mod_sub_i)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y~x) +
  xlab("Simulated random intercepts (sub_i)") +
  ylab("Modeled random intercepts")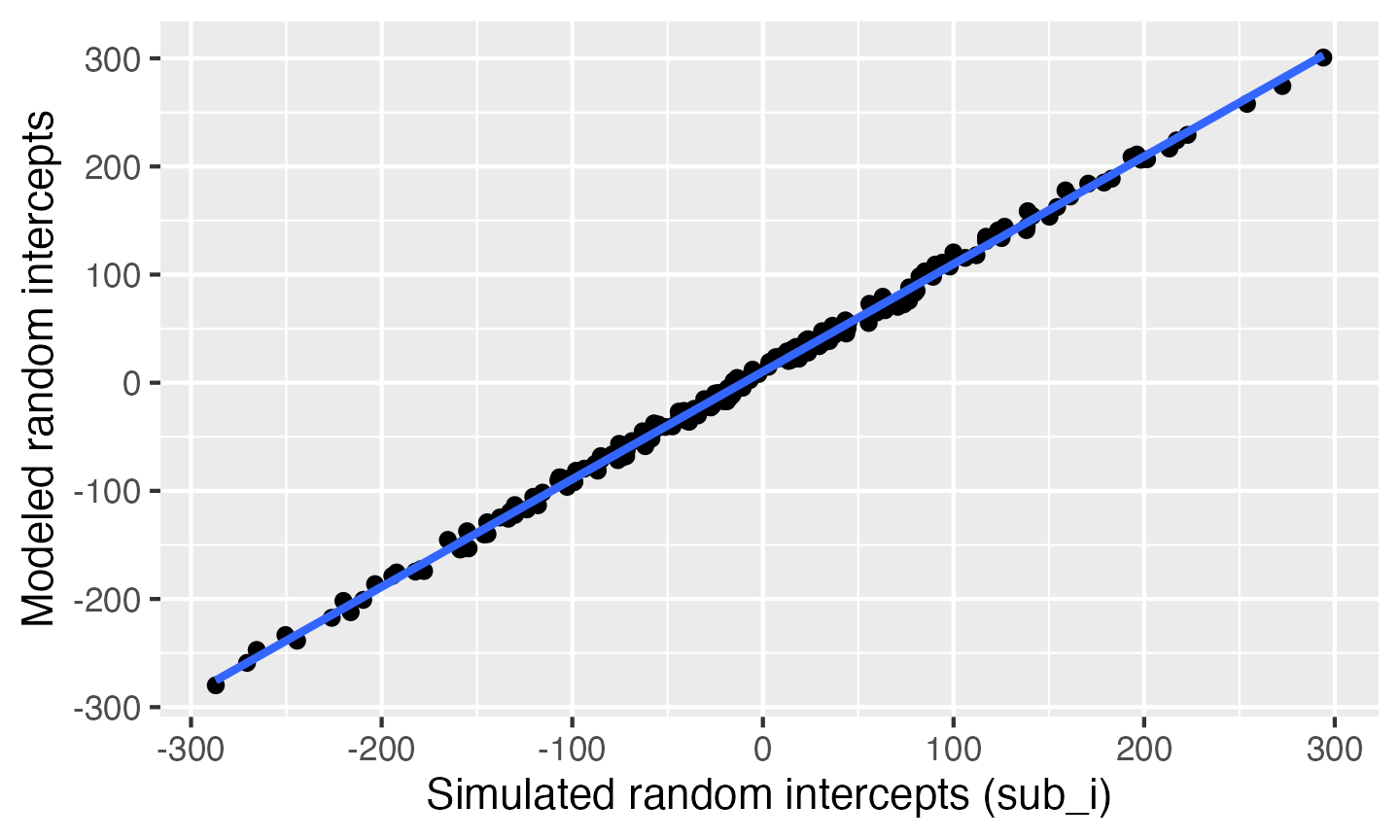

Compare simulated subject random intercepts to those from the model

Plot the stimulus intercepts from our code above (dat$stim_i) against the stimulus intercepts calculated by lmer (ranef(mod)$stim_id).

# get simulated random intercept for each stimulus
stim_sim <- dat |>
  group_by(stim, stim_i) |>
  summarise(.groups = "drop")

# join to calculated random intercept from model
stim_sim_mod <- ranef(mod)$stim |>
  as_tibble(rownames = "stim") |>
  rename(mod_stim_i = `(Intercept)`) |>
  left_join(stim_sim, by = "stim")

# plot to check correspondence
stim_sim_mod |>
  ggplot(aes(stim_i,mod_stim_i)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y~x) +
  xlab("Simulated random intercepts (stim_i)") +
  ylab("Modeled random intercepts")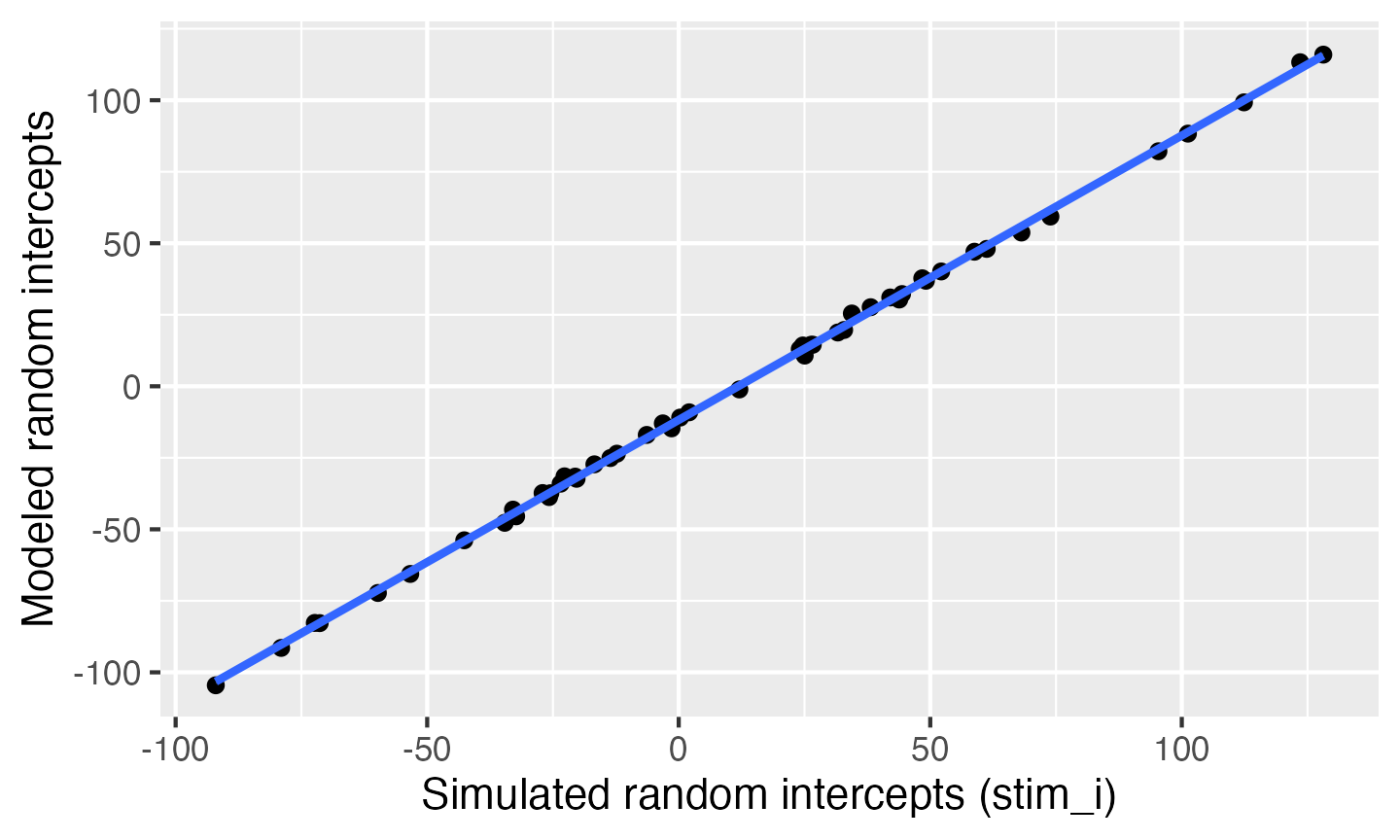

Compare simulated stimulus random intercepts to those from the model

Function

You can put the code above in a function so you can run it more easily and change the parameters. I removed the plot and set the argument defaults to the same as the example above with all fixed effects set to 0, but you can set them to other patterns.

sim_lmer <- function( sub_n = 200,
                      stim_n = 50,
                      sub_sd = 100,
                      stim_sd = 50,
                      error_sd = 25,
                      grand_i = 400,
                      cond_eff = 0,
                      vers_eff = 0, 
                      cond_vers_ixn = 0) {
  dat <- add_random(sub = sub_n) |>
    add_random(stim = stim_n) |>
    add_between(.by = "sub", condition = c("easy","hard")) |>
    add_within(version = c("congruent", "incongruent")) |>
    add_contrast("condition", colnames = "cond") |>
    add_contrast("version", colnames = "vers") |>
    add_ranef(.by = "sub", sub_i = sub_sd) |>
    add_ranef(.by = "stim", stim_i = stim_sd) |>
    add_ranef(err = error_sd) |>
    mutate(dv = grand_i + sub_i + stim_i + err +
           (cond * cond_eff) + 
           (vers * vers_eff) + 
           (cond * vers * cond_vers_ixn)
    )
  
  mod <- lmer(dv ~ cond * vers +
                (1 | sub) + 
                (1 | stim),
              data = dat)
  
  return(mod)
}

Run the function with the default values (so all fixed effects set to 0).

sim_lmer() %>% summary()
## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.00215933 (tol = 0.002, component 1)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: dv ~ cond * vers + (1 | sub) + (1 | stim)
##    Data: dat
## 
## REML criterion at convergence: 187222
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -4.191 -0.666  0.005  0.671  3.958 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sub      (Intercept) 11254    106.1   
##  stim     (Intercept)  3062     55.3   
##  Residual               620     24.9   
## Number of obs: 20000, groups:  sub, 200; stim, 50
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)   399.955     10.842   149.164   36.89   <2e-16 ***
## cond           14.384     15.007   198.045    0.96     0.34    
## vers           -0.111      0.352 19748.984   -0.31     0.75    
## cond:vers       0.817      0.705 19748.984    1.16     0.25    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) cond  vers 
## cond      0.000             
## vers      0.000  0.000      
## cond:vers 0.000  0.000 0.000
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00215933 (tol = 0.002, component 1)

Try changing some variables to simulate different patterns of fixed effects.

sim_lmer(cond_eff = 0,
         vers_eff = 75, 
         cond_vers_ixn = -50) %>%
  summary()
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: dv ~ cond * vers + (1 | sub) + (1 | stim)
##    Data: dat
## 
## REML criterion at convergence: 187381
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -4.761 -0.674 -0.007  0.665  3.875 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sub      (Intercept) 9410     97.0    
##  stim     (Intercept) 2260     47.5    
##  Residual              627     25.0    
## Number of obs: 20000, groups:  sub, 200; stim, 50
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)   396.707      9.606   160.846   41.30   <2e-16 ***
## cond           -9.966     13.723   198.000   -0.73     0.47    
## vers           75.323      0.354 19749.000  212.69   <2e-16 ***
## cond:vers     -49.997      0.708 19749.000  -70.59   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) cond  vers 
## cond      0.000             
## vers      0.000  0.000      
## cond:vers 0.000  0.000 0.000

Power analysis

First, wrap your simulation function inside of another function that takes the argument of a replication number, runs a simulated analysis, and returns a data table of the fixed and random effects (made with broom.mixed::tidy()). You can use purrr’s map_df() function to create a data table of results from multiple replications of this function. We’re only running 10 replications here in the interests of time, but you’ll want to run 100 or more for a proper power calculation.

sim_lmer_pwr <- function(rep) {
  s <- sim_lmer(cond_eff = 0,
                vers_eff = 75, 
                cond_vers_ixn = 50)
  
  # put just the fixed effects into a data table
  broom.mixed::tidy(s, "fixed") %>%
    mutate(rep = rep) # add a column for which rep
}

my_power <- map_df(1:10, sim_lmer_pwr)

You can then plot the distribution of estimates across your simulations.

ggplot(my_power, aes(estimate, color = term)) +
  geom_density() +
  facet_wrap(~term, scales = "free")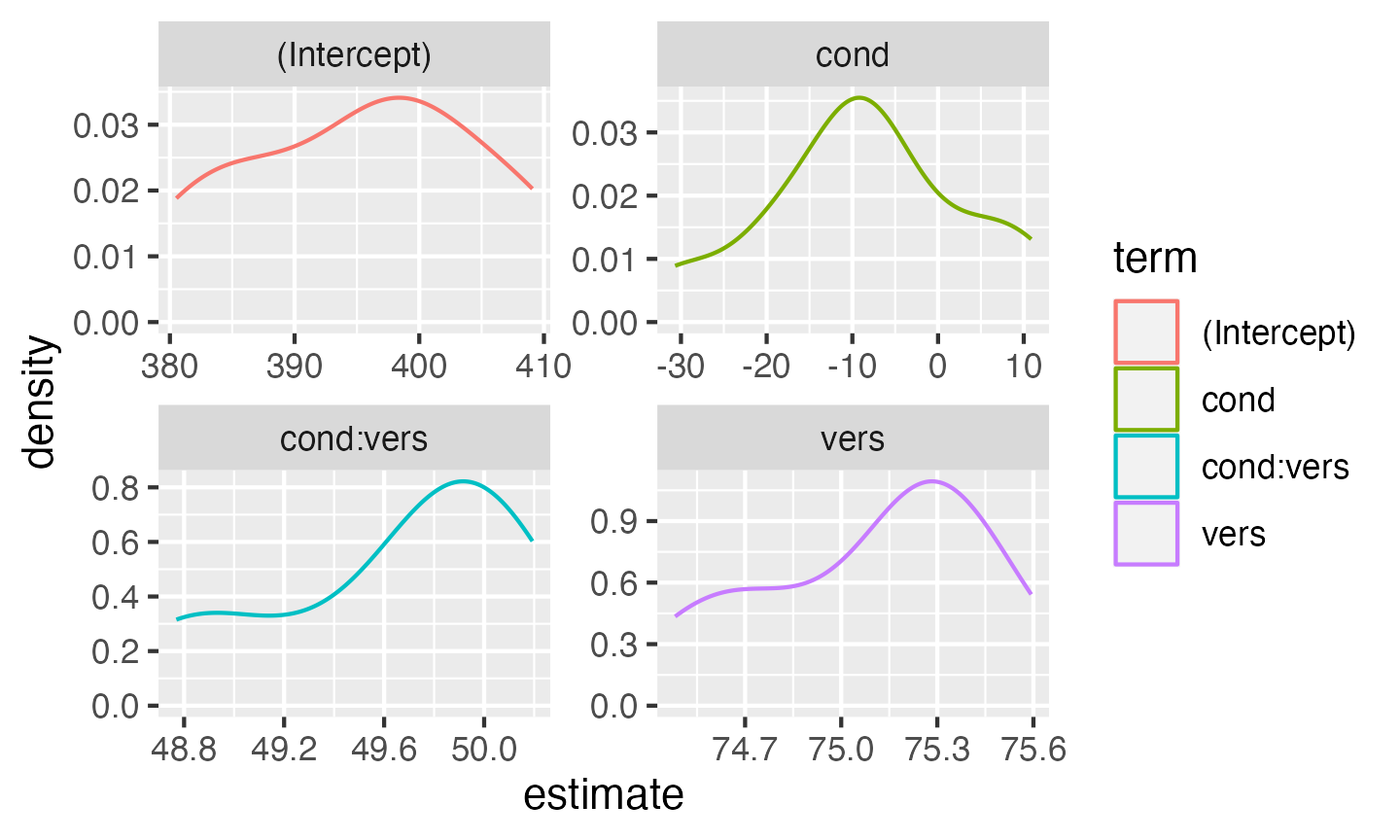

You can also just calculate power as the proportion of p-values less than your alpha.

my_power %>%
  group_by(term) %>%
  summarise(power = mean(p.value < 0.05),
            .groups = "drop")
## # A tibble: 4 × 2
##   term        power
##   <chr>       <dbl>
## 1 (Intercept)   1  
## 2 cond          0.1
## 3 cond:vers     1  
## 4 vers          1

Random slopes

In the example so far we’ve ignored random variation among subjects or stimuli in the size of the fixed effects (i.e., random slopes).

First, let’s reset the parameters we set above.

sub_n         <- 200 # number of subjects in this simulation
stim_n        <- 50  # number of stimuli in this simulation
sub_sd        <- 100 # SD for the subjects' random intercept
stim_sd       <- 50  # SD for the stimuli's random intercept
error_sd      <- 25  # residual (error) SD
grand_i       <- 400 # overall mean DV
cond_eff      <- 50  # mean difference between conditions: hard - easy
vers_eff      <- 50  # mean difference between versions: incongruent - congruent
cond_vers_ixn <-  0  # interaction between version and condition

Slopes

In addition to generating a random intercept for each subject, now we will also generate a random slope for any within-subject factors. The only within-subject factor in this design is version. The main effect of version is set to 50 above, but different subjects will show variation in the size of this effect. That’s what the random slope captures. We’ll set sub_vers_sd below to the SD of this variation and use this to calculate the random slope (sub_version_slope) for each subject.

Also, it’s likely that the variation between subjects in the size of the effect of version is related in some way to between-subject variation in the intercept. So we want the random intercept and slope to be correlated. Here, we’ll simulate a case where subjects who have slower (larger) reaction times across the board show a smaller effect of condition, so we set sub_i_vers_cor below to a negative number (-0.2).

We just have to edit the first add_ranef() to add two variables (sub_i, sub_vers_slope) that are correlated with r = -0.2, means of 0, and SDs equal to what we set sub_sd above and sub_vers_sd below.

sub_vers_sd <- 20
sub_i_vers_cor <- -0.2

dat <- add_random(sub = sub_n) |>
    add_random(stim = stim_n) |>
    add_between(.by = "sub", condition = c("easy","hard")) |>
    add_within(version = c("congruent", "incongruent")) |>
    add_contrast("condition", colnames = "cond") |>
    add_contrast("version", colnames = "vers") |>
    add_ranef(.by = "sub", sub_i = sub_sd, 
              sub_vers_slope = sub_vers_sd,
              .cors = sub_i_vers_cor)

Correlated Slopes

In addition to generating a random intercept for each stimulus, we will also generate a random slope for any within-stimulus factors. Both version and condition are within-stimulus factors (i.e., all stimuli are seen in both congruent and incongruent versions and both easy and hard conditions). So the main effects of version and condition (and their interaction) will vary depending on the stimulus.

They will also be correlated, but in a more complex way than above. You need to set the correlations for all pairs of slopes and intercept. Let’s set the correlation between the random intercept and each of the slopes to -0.4 and the slopes all correlate with each other +0.2 (You could set each of the six correlations separately if you want, though).

stim_vers_sd <- 10 # SD for the stimuli's random slope for stim_version
stim_cond_sd <- 30 # SD for the stimuli's random slope for sub_cond
stim_cond_vers_sd <- 15 # SD for the stimuli's random slope for sub_cond:stim_version
stim_i_cor <- -0.4 # correlations between intercept and slopes
stim_s_cor <- +0.2 # correlations among slopes

# specify correlations for rnorm_multi (one of several methods)
stim_cors <- c(stim_i_cor, stim_i_cor, stim_i_cor,
                           stim_s_cor, stim_s_cor,
                                       stim_s_cor)

dat <- add_random(sub = sub_n) |>
    add_random(stim = stim_n) |>
    add_between(.by = "sub", condition = c("easy","hard")) |>
    add_within(version = c("congruent", "incongruent")) |>
    add_contrast("condition", colnames = "cond") |>
    add_contrast("version", colnames = "vers") |>
    add_ranef(.by = "sub", sub_i = sub_sd, 
              sub_vers_slope = sub_vers_sd,
              .cors = sub_i_vers_cor) |>
    add_ranef(.by = "stim", stim_i = stim_sd,
              stim_vers_slope = stim_vers_sd,
              stim_cond_slope = stim_cond_sd,
              stim_cond_vers_slope = stim_cond_vers_sd,
              .cors = stim_cors)

Calculate DV

Now we can calculate the DV by adding together an overall intercept (mean RT for all trials), the subject-specific intercept, the stimulus-specific intercept, the effect of subject condition, the stimulus-specific slope for condition, the effect of stimulus version, the stimulus-specific slope for version, the subject-specific slope for condition, the interaction between condition and version (set to 0 for this example), the stimulus-specific slope for the interaction between condition and version, and an error term.

dat <- add_random(sub = sub_n) |>
    add_random(stim = stim_n) |>
    add_between(.by = "sub", condition = c("easy","hard")) |>
    add_within(version = c("congruent", "incongruent")) |>
    add_contrast("condition", colnames = "cond") |>
    add_contrast("version", colnames = "vers") |>
    add_ranef(.by = "sub", sub_i = sub_sd, 
              sub_vers_slope = sub_vers_sd,
              .cors = sub_i_vers_cor) |>
    add_ranef(.by = "stim", stim_i = stim_sd,
              stim_vers_slope = stim_vers_sd,
              stim_cond_slope = stim_cond_sd,
              stim_cond_vers_slope = stim_cond_vers_sd,
              .cors = stim_cors) |>
    add_ranef(err = error_sd) |>
  mutate(
    trial_cond_eff = cond_eff + stim_cond_slope,
    trial_vers_eff = vers_eff + sub_vers_slope + stim_vers_slope,
    trial_cond_vers_ixn = cond_vers_ixn + stim_cond_vers_slope,
    dv = grand_i + sub_i + stim_i + err +
         (cond * trial_cond_eff) + 
         (vers * trial_vers_eff) + 
         (cond * vers * trial_cond_vers_ixn)
  )

As always, graph to make sure you’ve simulated the general pattern you expected.

ggplot(dat, aes(condition, dv, color = version)) +
  geom_hline(yintercept = grand_i) +
  geom_violin(alpha = 0.5) +
  stat_summary(fun = mean,
               fun.min = \(x){mean(x) - sd(x)},
               fun.max = \(x){mean(x) + sd(x)},
               position = position_dodge(width = 0.9)) +
  scale_color_brewer(palette = "Dark2")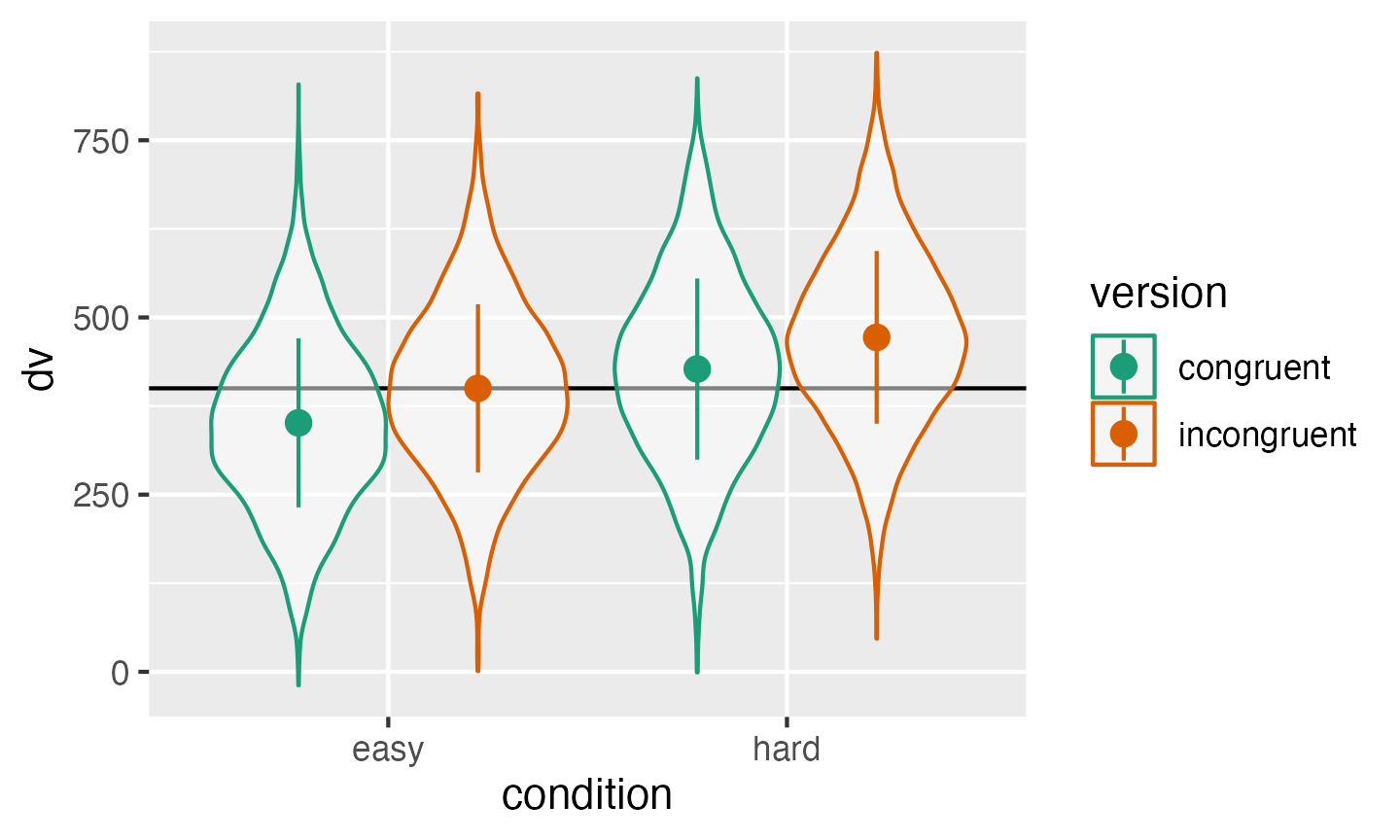

Double-check the simulated pattern

Analysis

New we’ll run a linear mixed effects model with lmer and look at the summary. You specify random slopes by adding the within-level effects to the random intercept specifications. Since the only within-subject factor is version, the random effects specification for subjects is (1 + vers | sub). Since both condition and version are within-stimuli factors, the random effects specification for stimuli is (1 + vers*cond | stim).

This model will take a lot longer to run than one without random slopes specified. This might be a good time for a coffee break.

mod <- lmer(dv ~ cond * vers +
              (1 + vers || sub) + 
              (1 + vers*cond || stim),
            data = dat)

mod.sum <- summary(mod)

mod.sum
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: dv ~ cond * vers + (1 + vers || sub) + (1 + vers * cond || stim)
##    Data: dat
## 
## REML criterion at convergence: 188362
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -3.713 -0.672  0.003  0.667  3.928 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sub      (Intercept) 9969.0   99.84   
##  sub.1    vers         369.5   19.22   
##  stim     (Intercept) 4055.8   63.68   
##  stim.1   vers          81.7    9.04   
##  stim.2   cond        1099.1   33.15   
##  stim.3   vers:cond    225.7   15.02   
##  Residual              623.8   24.98   
## Number of obs: 20000, groups:  sub, 200; stim, 50
## 
## Fixed effects:
##             Estimate Std. Error     df t value  Pr(>|t|)    
## (Intercept)   412.57      11.45 116.78   36.05   < 2e-16 ***
## cond           73.93      14.88 232.50    4.97 0.0000013 ***
## vers           46.66       1.90 157.13   24.57   < 2e-16 ***
## cond:vers      -4.00       3.52 185.98   -1.14      0.26    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) cond  vers 
## cond      0.000             
## vers      0.000  0.000      
## cond:vers 0.000  0.000 0.000

Sense checks

First, check that your groups make sense.

• sub = sub_n (200)
• stim = stim_n (50)

mod.sum$ngrps |>
  as_tibble(rownames = "Random.Fator") |>
  mutate(parameters = c(sub_n, stim_n))
## # A tibble: 2 × 3
##   Random.Fator value parameters
##   <chr>        <dbl>      <dbl>
## 1 sub            200        200
## 2 stim            50         50

Next, look at the SDs for the random effects.

• Group:sub
  • (Intercept) ~= sub_sd
  • vers ~= sub_vers_sd
• Group: stim
  • (Intercept) ~= stim_sd
  • vers ~= stim_vers_sd
  • cond ~= stim_cond_sd
  • vers:cond ~= stim_cond_vers_sd
• Residual ~= error_sd

mod.sum$varcor |>
  as_tibble() |>
  select(Groups = grp, Name = var1, "Std.Dev." = sdcor) |>
  mutate(parameters = c(sub_sd, sub_vers_sd, stim_sd, stim_vers_sd, stim_cond_sd, stim_cond_vers_sd, error_sd))
## # A tibble: 7 × 4
##   Groups   Name        Std.Dev. parameters
##   <chr>    <chr>          <dbl>      <dbl>
## 1 sub      (Intercept)    99.8         100
## 2 sub.1    vers           19.2          20
## 3 stim     (Intercept)    63.7          50
## 4 stim.1   vers            9.04         10
## 5 stim.2   cond           33.2          30
## 6 stim.3   vers:cond      15.0          15
## 7 Residual NA             25.0          25

The correlations are a bit more difficult to parse. The first column under Corr shows the correlation between the random slope for that row and the random intercept. So for vers under sub, the correlation should be close to sub_i_vers_cor. For all three random slopes under stim, the correlation with the random intercept should be near stim_i_cor and their correlations with each other should be near stim_s_cor.

Finally, look at the fixed effects.

• (Intercept) ~= grand_i
• sub_cond.e ~= sub_cond_eff
• stim_version.e ~= stim_vers_eff
• sub_cond.e:stim_version.e ~= cond_vers_ixn

mod.sum$coefficients |>
  as_tibble(rownames = "Effect") |>
  select(Effect, Estimate) |>
  mutate(parameters = c(grand_i, cond_eff, vers_eff, cond_vers_ixn))
## # A tibble: 4 × 3
##   Effect      Estimate parameters
##   <chr>          <dbl>      <dbl>
## 1 (Intercept)   413.          400
## 2 cond           73.9          50
## 3 vers           46.7          50
## 4 cond:vers      -4.00          0

Function

You can put the code above in a function so you can run it more easily and change the parameters. I removed the plot and set the argument defaults to the same as the example above, but you can set them to other patterns.

sim_lmer_slope <- function( sub_n = 200,
                            stim_n = 50,
                            sub_sd = 100,
                            sub_vers_sd = 20, 
                            sub_i_vers_cor = -0.2,
                            stim_sd = 50,
                            stim_vers_sd = 10,
                            stim_cond_sd = 30,
                            stim_cond_vers_sd = 15,
                            stim_i_cor = -0.4,
                            stim_s_cor = +0.2,
                            error_sd = 25,
                            grand_i = 400,
                            sub_cond_eff = 0,
                            stim_vers_eff = 0, 
                            cond_vers_ixn = 0) {
  dat <- add_random(sub = sub_n) |>
    add_random(stim = stim_n) |>
    add_between(.by = "sub", condition = c("easy","hard")) |>
    add_within(version = c("congruent", "incongruent")) |>
    add_contrast("condition", colnames = "cond") |>
    add_contrast("version", colnames = "vers") |>
    add_ranef(.by = "sub", sub_i = sub_sd, 
              sub_vers_slope = sub_vers_sd,
              .cors = sub_i_vers_cor) |>
    add_ranef(.by = "stim", stim_i = stim_sd,
              stim_vers_slope = stim_vers_sd,
              stim_cond_slope = stim_cond_sd,
              stim_cond_vers_slope = stim_cond_vers_sd,
              .cors = stim_cors) |>
    add_ranef(err = error_sd) |>
    mutate(
      trial_cond_eff = cond_eff + stim_cond_slope,
      trial_vers_eff = vers_eff + sub_vers_slope + stim_vers_slope,
      trial_cond_vers_ixn = cond_vers_ixn + stim_cond_vers_slope,
      dv = grand_i + sub_i + stim_i + err +
           (cond * trial_cond_eff) + 
           (vers * trial_vers_eff) + 
           (cond * vers * trial_cond_vers_ixn)
    )
  
  mod <- lmer(dv ~ cond * vers +
                (1 + vers || sub) + 
                (1 + vers*cond || stim),
              data = dat)
  
  return(mod)
}

Run the function with the default values (null fixed effects).

sim_lmer_slope() %>% summary()
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: dv ~ cond * vers + (1 + vers || sub) + (1 + vers * cond || stim)
##    Data: dat
## 
## REML criterion at convergence: 188480
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -3.865 -0.661 -0.001  0.667  3.989 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sub      (Intercept) 9836.4   99.18   
##  sub.1    vers         363.3   19.06   
##  stim     (Intercept) 2008.3   44.81   
##  stim.1   vers          97.1    9.85   
##  stim.2   cond         972.5   31.18   
##  stim.3   vers:cond    206.3   14.36   
##  Residual              629.0   25.08   
## Number of obs: 20000, groups:  sub, 200; stim, 50
## 
## Fixed effects:
##             Estimate Std. Error     df t value Pr(>|t|)    
## (Intercept)   393.75       9.45 176.71   41.65  < 2e-16 ***
## cond           51.31      14.71 229.84    3.49  0.00058 ***
## vers           46.13       1.97 141.94   23.41  < 2e-16 ***
## cond:vers      -2.55       3.45 190.63   -0.74  0.45979    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) cond  vers 
## cond      0.000             
## vers      0.000  0.000      
## cond:vers 0.000  0.000 0.000

Try changing some variables to simulate fixed effects.

sim_lmer_slope(sub_cond_eff = 50,
               stim_vers_eff = 50, 
               cond_vers_ixn = 0)
## Linear mixed model fit by REML ['lmerModLmerTest']
## Formula: dv ~ cond * vers + (1 + vers || sub) + (1 + vers * cond || stim)
##    Data: dat
## REML criterion at convergence: 188364
## Random effects:
##  Groups   Name        Std.Dev.
##  sub      (Intercept) 102.79  
##  sub.1    vers         20.38  
##  stim     (Intercept)  54.20  
##  stim.1   vers          9.05  
##  stim.2   cond         31.91  
##  stim.3   vers:cond    16.82  
##  Residual              24.96  
## Number of obs: 20000, groups:  sub, 200; stim, 50
## Fixed Effects:
## (Intercept)         cond         vers    cond:vers  
##      404.57        60.31        46.06        -2.81

Exercises

1. Calculate power for the parameters in the last example using the sim_lmer_slope() function.

2. Simulate data for the following design:

• 100 raters rate 50 faces from group A and 50 faces from group B
• The DV has a mean value of 50
• Group B values are 5 points higher than group A
• Rater intercepts have an SD of 5
• Face intercepts have an SD of 10
• The residual error has an SD of 8

3. For the design from exercise 2, write a function that simulates data and runs a mixed effects analysis on it.

4. The package faux has a built-in dataset called fr4. Type ?faux::fr4 into the console to view the help for this dataset. Run a mixed effects model on this dataset looking at the effect of face_sex on ratings. Remember to include a random slope for the effect of face sex and explicitly add a contrast code.

5. Use the parameters from this analysis to simulate a new dataset with 50 male and 50 female faces, and 100 raters.