Contrasts

Source: vignettes/contrasts.Rmd

Contrasts other than treatment coding for factors with more than two levels have always confused me. I try to design all my own studies to never have more than two levels per categorical factor, but students in my data skills class are always trying to analyse data with three-level categories (or worse).

I thought it was just me, but some recent Twitter discussion showed me I’m not alone. There’s a serious jingle-jangle problem with contrasts. Here are some of the explainers that I found useful (thanks to everyone who recommended them).

  1. Contrasts in R by Marissa Barlaz
  2. Coding categorical predictor variables in factorial designs by Dale Barr
  3. Contrast Coding in Multiple Regression Analysis by Matthew Davis
  4. R Library Contrast Coding Systems for categorical variables by UCLA Statistical Consulting
  5. Rosetta store: Contrasts by GAMLj
  6. Coding Schemes for Categorical Variables by Phillip Alday
  7. Experimental personality designs: analyzing categorical by continuous variable interactions by West, Aiken & Krull

Terminology

Contrasts often have multiple names. The names I’m using try to maintain the relationship with the base R function, apart from anova coding, which was suggested by Dale Barr after I got frustrated that people use so many different labels for that (extremely useful) coding and each of the terms used is also used to refer to totally different codings by others.

My name Other names R function faux function
Treatment Treatment (2), Dummy (1, 4, 6), Simple (5) contr.treatment contr_code_treatment
Anova Deviation (2), Contrast (1), Simple (4) contr.treatment - 1/k contr_code_anova
Sum Sum (1, 2, 6), Effects (3), Deviation (4, 5), Unweighted Effects (7) contr.sum contr_code_sum
Difference Contrast (3), Forward/Backward (4), Repeated (5) MASS::contr.sdif contr_code_difference
Helmert Reverse Helmert (1, 4), Difference (5), Contrast (7) contr.helmert / (column_i+1) contr_code_helmert
Polynomial Polynomial (5), Orthogonal Polynomial (4), Trend (3) contr.poly contr_code_poly

Faux Contrast Functions

These functions are under development

First, we’ll set up a simple experimental design and analyse it with lm(). I set empirical = TRUE to make interpreting the estimates easier.

df <- sim_design(between = list(pet = c("cat", "dog", "ferret")), 
                 n = c(50), mu = c(2, 4, 9), empirical = TRUE)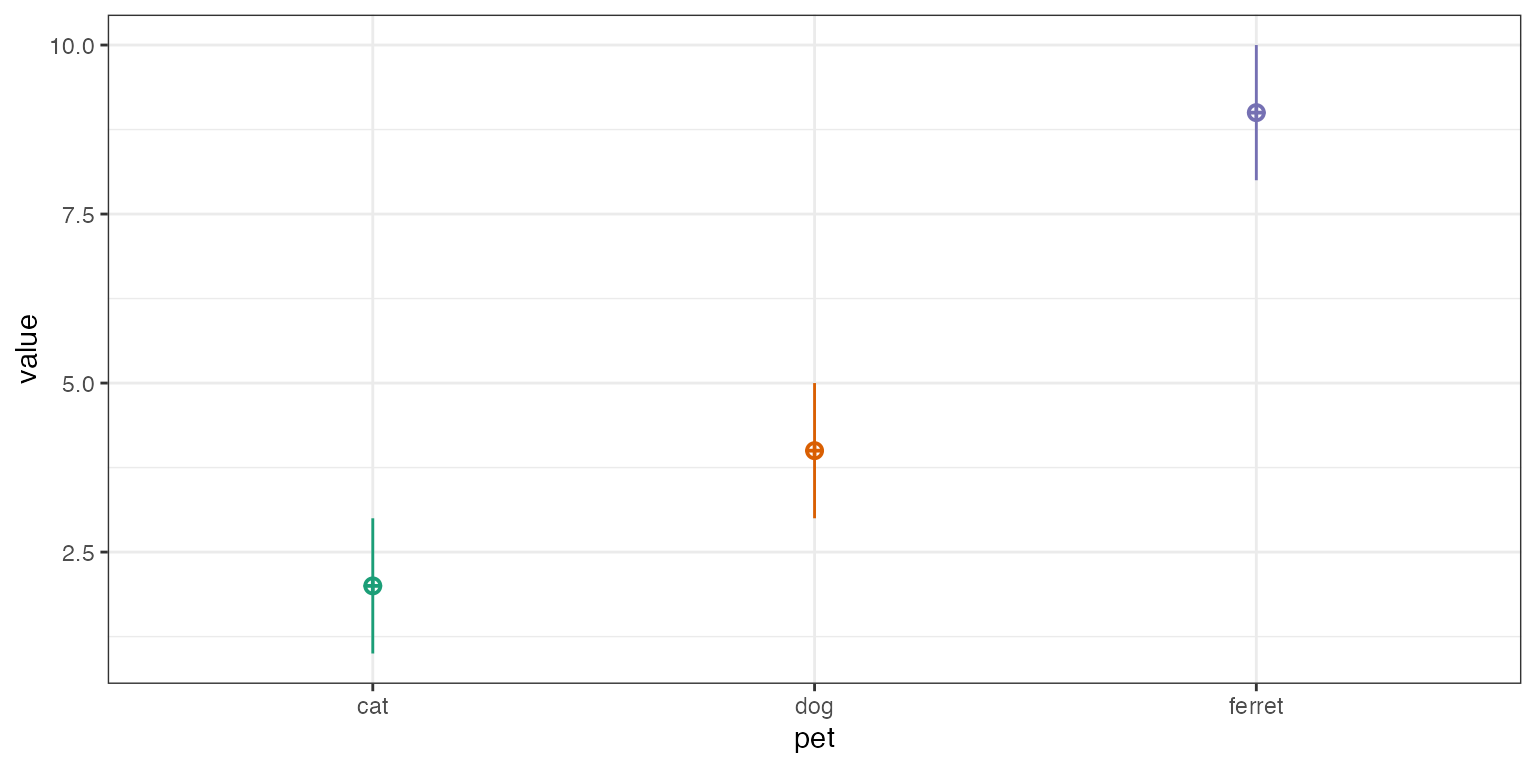

Notice that the default contrast is treatment coding, with “cat” as the baseline condition. The estimate for the intercept is the mean value for cats (\(2\)), while the term petdog is the mean value for dogs minus cats (\(4 - 2\)), and the term petferret is the mean value for ferrets minus cats (\(9 - 2\)).

Contrasts lm(y ~ pet, df)
dog ferret
cat 0 0
dog 1 0
ferret 0 1
term estimate std.error statistic p.value
(Intercept) 2 0.141 14.1 0
petdog 2 0.200 10.0 0
petferret 7 0.200 35.0 0

In all the subsequent examples, try putting into words what the estimates for the intercept and terms mean in relation to the mean values for each group in the data.

Treatment

Treatment coding (also called dummy coding) sets the mean of the reference group as the intercept. It is straightforward to interpret, especially when your factors have an obvious default or baseline value. This is the same type of coding as the default for factors shown above (unless you change your default using options()), but with clearer term labels.

df$pet <- contr_code_treatment(df$pet)
Contrasts lm(y ~ pet, df)
.dog-cat .ferret-cat
cat 0 0
dog 1 0
ferret 0 1
term estimate std.error statistic p.value
(Intercept) 2 0.141 14.1 0
pet.dog-cat 2 0.200 10.0 0
pet.ferret-cat 7 0.200 35.0 0

Each contrast compares one level with the reference level, which defaults to the first level, but you can set with the base argument. Now the intercept estimates the mean value for dogs (\(4\)).

df$pet <- contr_code_treatment(df$pet, base = "dog")
Contrasts lm(y ~ pet, df)
.cat-dog .ferret-dog
cat 1 0
dog 0 0
ferret 0 1
term estimate std.error statistic p.value
(Intercept) 4 0.141 28.3 0
pet.cat-dog -2 0.200 -10.0 0
pet.ferret-dog 5 0.200 25.0 0

Set the reference level to the third level (“ferret”).

df$pet <- contr_code_treatment(df$pet, base = 3)
Contrasts lm(y ~ pet, df)
.cat-ferret .dog-ferret
cat 1 0
dog 0 1
ferret 0 0
term estimate std.error statistic p.value
(Intercept) 9 0.141 63.6 0
pet.cat-ferret -7 0.200 -35.0 0
pet.dog-ferret -5 0.200 -25.0 0

Anova

Anova coding is identical to treatment coding, but sets the grand mean as the intercept. Each contrast compares one level with a reference level. This gives us values that are relatively easy to interpret and map onto ANOVA values.

Below is anova coding with the first level (“cat”) as the default base. Now the intercept is the grand mean, which is the mean of the three group means (\((2 + 4 + 9)/3\)). Notice that this is different from the mean value of y in our dataset (5, since the number of pets in each group is unbalanced. The term pet_dog-cat is the mean value for dogs minus cats (\(4 - 2\)) and the term pet_ferret-cat is the mean value for ferrets minus cats (\(9 - 2\)).

df$pet <- contr_code_anova(df$pet)
Contrasts lm(y ~ pet, df)
.dog-cat .ferret-cat
cat -0.333 -0.333
dog 0.667 -0.333
ferret -0.333 0.667
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.dog-cat 2 0.200 10.0 0
pet.ferret-cat 7 0.200 35.0 0

Anova coding with “dog” as the base. How does the interpretation of the terms change?

df$pet <- contr_code_anova(df$pet, base = "dog")
Contrasts lm(y ~ pet, df)
.cat-dog .ferret-dog
cat 0.667 -0.333
dog -0.333 -0.333
ferret -0.333 0.667
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.cat-dog -2 0.200 -10.0 0
pet.ferret-dog 5 0.200 25.0 0

Anova coding with the third level (“ferret”) as the base.

df$pet <- contr_code_anova(df$pet, base = 3)
Contrasts lm(y ~ pet, df)
.cat-ferret .dog-ferret
cat 0.667 -0.333
dog -0.333 0.667
ferret -0.333 -0.333
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.cat-ferret -7 0.200 -35.0 0
pet.dog-ferret -5 0.200 -25.0 0

Sum

Sum coding also sets the grand mean as the intercept. Each contrast compares one level with the grand mean. Therefore, the estimate for pet_cat-intercept is the difference between the mean value for cats and the grand mean (\(2 - 5\)).

df$pet <- contr_code_sum(df$pet)
Contrasts lm(y ~ pet, df)
.cat-intercept .dog-intercept
cat 1 0
dog 0 1
ferret -1 -1
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.24 0
pet.cat-intercept -3 0.115 -25.98 0
pet.dog-intercept -1 0.115 -8.66 0

You can’t compare all levels with the grand mean, and have to omit one level. This is the last level by default, but you can change it with the omit argument.

df$pet <- contr_code_sum(df$pet, omit = "dog")
Contrasts lm(y ~ pet, df)
.cat-intercept .ferret-intercept
cat 1 0
dog -1 -1
ferret 0 1
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.cat-intercept -3 0.115 -26.0 0
pet.ferret-intercept 4 0.115 34.6 0

Omit the first level (“cat”).

df$pet <- contr_code_sum(df$pet, omit = 1)
Contrasts lm(y ~ pet, df)
.dog-intercept .ferret-intercept
cat -1 -1
dog 1 0
ferret 0 1
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.24 0
pet.dog-intercept -1 0.115 -8.66 0
pet.ferret-intercept 4 0.115 34.64 0

Difference

A slightly different form of contrast coding is difference coding, also called forward, backward, or successive differences coding. It compares each level to the previous one, rather than to a baseline level.

df$pet <- contr_code_difference(df$pet)
Contrasts lm(y ~ pet, df)
.dog-cat .ferret-dog
cat -0.667 -0.333
dog 0.333 -0.333
ferret 0.333 0.667
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.dog-cat 2 0.200 10.0 0
pet.ferret-dog 5 0.200 25.0 0

If you want to change which levels are compared, you can re-order the factor levels.

df$pet <- contr_code_difference(df$pet, levels = c("ferret", "cat", "dog"))
Contrasts lm(y ~ pet, df)
.cat-ferret .dog-cat
ferret -0.667 -0.333
cat 0.333 -0.333
dog 0.333 0.667
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.cat-ferret -7 0.200 -35.0 0
pet.dog-cat 2 0.200 10.0 0

Helmert

Helmert coding sets the grand mean as the intercept. Each contrast compares one level with the mean of previous levels. This coding is somewhat different than the results from stats::contr.helmert() to make it easier to interpret the estimates. Thus, pet_ferret-cat.dog is the mean value for ferrets minus the mean value for cats and dogs averaged together (\(9-(2+4)/2\)).

df$pet <- contr_code_helmert(df$pet)
Contrasts lm(y ~ pet, df)
.dog-cat .ferret-cat.dog
cat -0.5 -0.333
dog 0.5 -0.333
ferret 0.0 0.667
term estimate std.error statistic p.value
(Intercept) 5 0.082 61.2 0
pet.dog-cat 2 0.200 10.0 0
pet.ferret-cat.dog 6 0.173 34.6 0

You can change the comparisons by reordering the levels.

df$pet <- contr_code_helmert(df$pet, levels = c("ferret", "dog", "cat"))
Contrasts lm(y ~ pet, df)
.dog-ferret .cat-ferret.dog
ferret -0.5 -0.333
dog 0.5 -0.333
cat 0.0 0.667
term estimate std.error statistic p.value
(Intercept) 5.0 0.082 61.2 0
pet.dog-ferret -5.0 0.200 -25.0 0
pet.cat-ferret.dog -4.5 0.173 -26.0 0

Polynomial

Polynomial coding is the default for ordered factors in R. We’ll set up a new data simulation with five ordered times.

df <- sim_design(list(time = 1:5),
                 mu = 1:5 * 0.25 + (1:5 - 3)^2 * 0.5,
                 sd = 5, long = TRUE)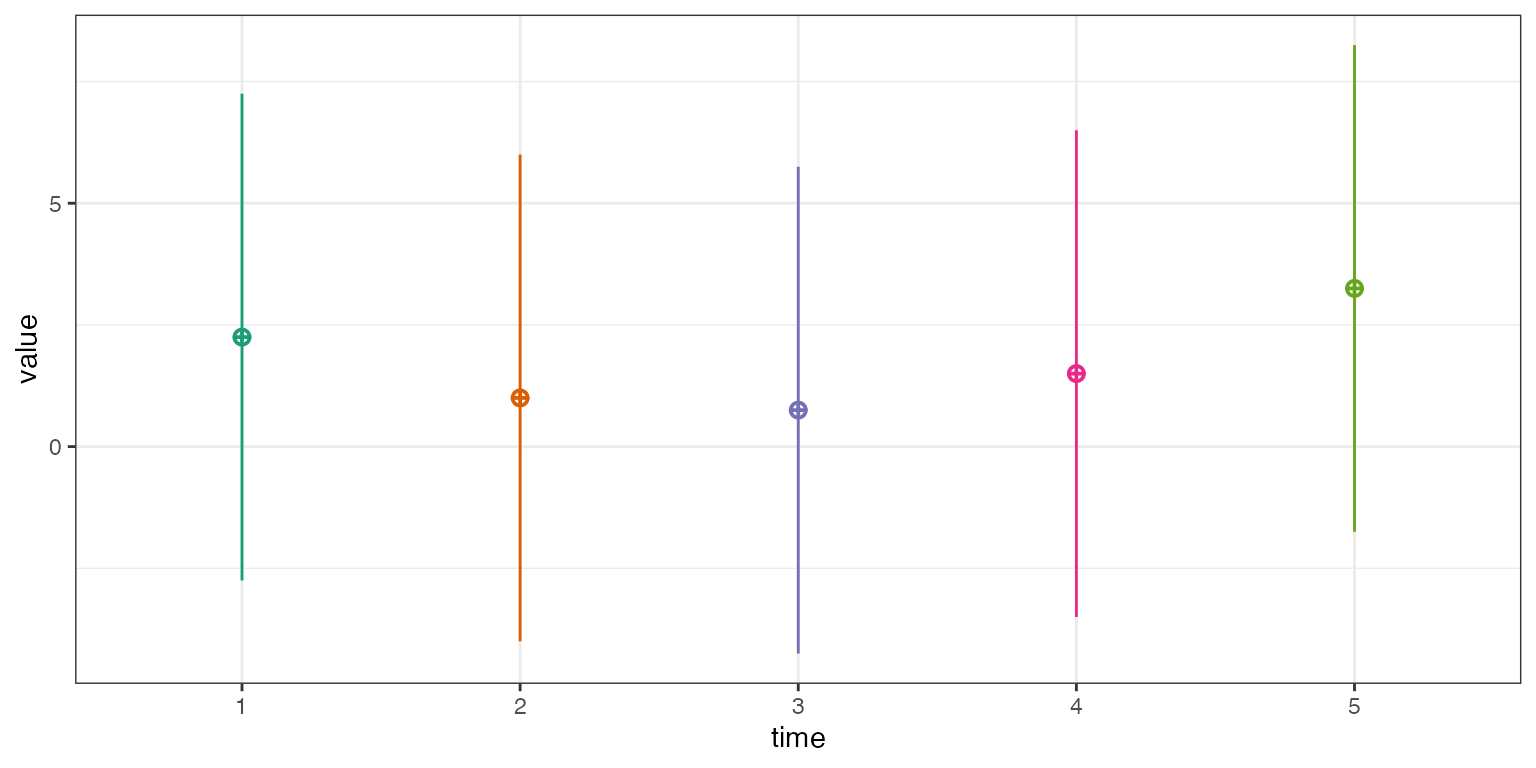

The function contr_code_poly() uses contr.poly() to set up the polynomial contrasts for the linear (^1), quadratic (^2), cubic (^3), and quartic (^4) components.

df$time <- contr_code_poly(df$time)
Contrasts lm(y ~ pet, df)
^1 ^2 ^3 ^4
-0.632 0.535 -0.316 0.120
-0.316 -0.267 0.632 -0.478
0.000 -0.535 0.000 0.717
0.316 -0.267 -0.632 -0.478
0.632 0.535 0.316 0.120
term estimate std.error statistic p.value
(Intercept) 2.031 0.223 9.110 0.000
time^1 0.239 0.498 0.480 0.631
time^2 1.946 0.498 3.905 0.000
time^3 -0.198 0.498 -0.397 0.692
time^4 -0.004 0.498 -0.009 0.993

Add Contrasts

The function add_contrasts() lets you add contrasts to a column in a data frame and also adds new columns for each contrast (unless add_cols = FALSE). This is especially helpful if you want to test only a subset of the contrasts.

df <- sim_design(list(time = 1:5),
                 mu = 1:5 * 0.25 + (1:5 - 3)^2 * 0.5,
                 sd = 5, long = TRUE, plot = FALSE) %>%
  add_contrast("time", "poly")
# test only the linear and quadratic contrasts
lm(y ~ `time^1` + `time^2`, df) %>% broom::tidy()
term estimate std.error statistic p.value
(Intercept) 1.69 0.239 7.09 0.000
time^1 0.78 0.534 1.46 0.145
time^2 2.06 0.534 3.85 0.000

You can set colnames to change the default column names for the contrasts. This can be useful if you want to add different codings for the same factor or if the default names are too long.

btwn <- list(condition = c("control", "experimental")) 

df <- sim_design(between = btwn, n = 1, plot = FALSE) %>%
  add_contrast("condition", "treatment", colnames = "cond.tr") %>%
  add_contrast("condition", "anova", colnames = "cond.aov") %>%
  add_contrast("condition", "difference", colnames = "cond.dif") %>%
  add_contrast("condition", "sum", colnames = "cond.sum") %>%
  add_contrast("condition", "helmert", colnames = "cond.hmt") %>%
  add_contrast("condition", "poly", colnames = "cond.poly")
id condition y cond.tr cond.aov cond.dif cond.sum cond.hmt cond.poly
S1 control 0.697 0 -0.5 -0.5 1 -0.5 -0.707
S2 experimental 0.512 1 0.5 0.5 -1 0.5 0.707

However, if a new column has a duplicate name to an existing column, add_contrast() will automatically add a contrast suffix to the new column.

btwn <- list(pet = c("cat", "dog", "ferret")) 

df <- sim_design(between = btwn, n = 1, plot = FALSE) %>%
  add_contrast("pet", "treatment") %>% 
  add_contrast("pet", "anova") %>%
  add_contrast("pet", "sum") %>%
  add_contrast("pet", "difference") %>%
  add_contrast("pet", "helmert") %>%
  add_contrast("pet", "poly")
id pet y pet.dog-cat pet.ferret-cat pet.dog-cat.aov pet.ferret-cat.aov pet.cat-intercept pet.dog-intercept pet.dog-cat.dif pet.ferret-dog pet.dog-cat.hmt pet.ferret-cat.dog pet^1 pet^2
S1 cat -0.72 0 0 -0.33 -0.33 1 0 -0.67 -0.33 -0.5 -0.33 -0.71 0.41
S2 dog -0.36 1 0 0.67 -0.33 0 1 0.33 -0.33 0.5 -0.33 0.00 -0.82
S3 ferret -1.43 0 1 -0.33 0.67 -1 -1 0.33 0.67 0.0 0.67 0.71 0.41

Examples

2x2 Design

Let’s use simulated data with empirical = TRUE to explore how to interpret interactions between two 2-level factors coded in different ways.

mu <- c(0, 4, 6, 10)
df <- sim_design(between = list(time = c("am", "pm"),
                                pet = c("cat", "dog")),
                 n = c(50, 60, 70, 80), mu = mu, empirical = TRUE)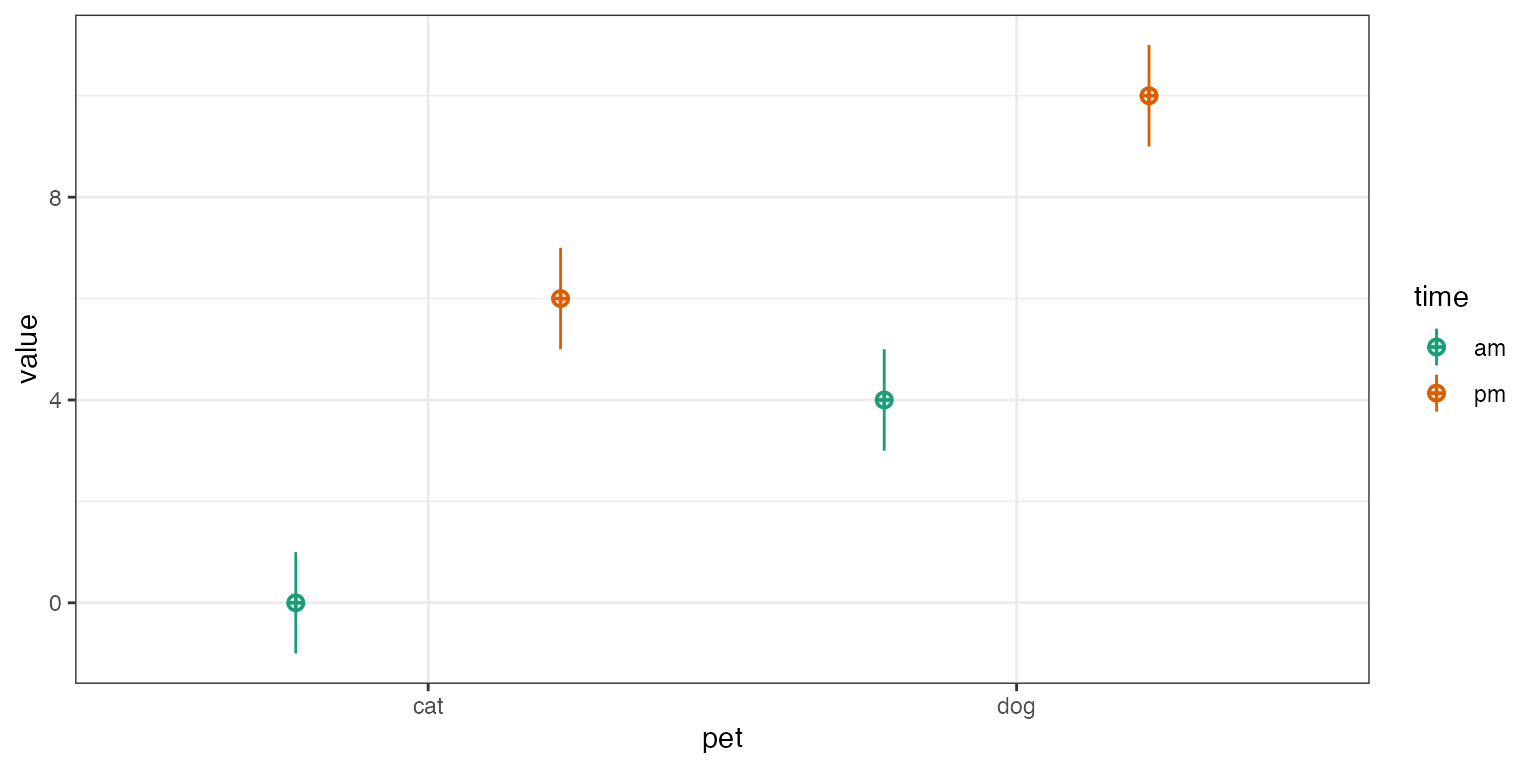

The table below shows the cell and marginal means. The notation \(Y_{..}\) is used to denote a mean for a specific grouping. The . is used to indicate the mean over all groups of that factor; Y.. is the grand mean. While you’ll usually see the subscripts written as numbers to indicate the factor levels, we’re using letters here so you don’t have to keep referring to the order of factors and levels.

cat dog mean
am \(Y_{ca} = 0\) \(Y_{da} = 4\) \(Y_{.a} = 2\)
pm \(Y_{cp} = 6\) \(Y_{dp} = 10\) \(Y_{.p} = 8\)
mean \(Y_{c.} = 3\) \(Y_{d.} = 7\) \(Y_{..} = 5\)

Treatment
term interpretation formula value
intercept cat when am \(Y_{ca}\) \(0\)
pet.dog-cat dog minus cat, when am \(Y_{da} - Y_{ca}\) \(4 - 0 = 4\)
time.pm-am pm minus am, for cats \(Y_{cp} - Y_{ca}\) \(6 - 0 = 6\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((10 - 6) - (4 - 0) = 0\) 
df %>%
  add_contrast("pet", "treatment") %>%
  add_contrast("time", "treatment") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 0 0.141 0.0 1
pet.dog-cat 4 0.191 20.9 0
time.pm-am 6 0.185 32.4 0
pet.dog-cat:time.pm-am 0 0.252 0.0 1
Anova
term interpretation formula value
intercept grand mean \(Y_{..}\) \(5\)
pet.dog-cat mean dog minus mean cat \(Y_{d.} - Y_{c.}\) \(7 - 3 = 4\)
time.pm-am mean pm minus mean am \(Y_{.p} - Y_{.a}\) \(8 - 2 = 6\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((10 - 6) - (4 - 0) = 0\) 
df %>%
  add_contrast("pet", "anova") %>%
  add_contrast("time", "anova") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 5 0.063 79.4 0
pet.dog-cat 4 0.126 31.8 0
time.pm-am 6 0.126 47.6 0
pet.dog-cat:time.pm-am 0 0.252 0.0 1
Sum
term interpretation formula value
intercept grand mean \(Y_{..}\) \(3\)
pet.cat-intercept mean cat minus grand mean \(Y_{c.} - Y_{..}\) \(3 - 5 = -2\)
time.am-intercept mean am minus grand mean \(Y_{.a} - Y_{..}\) \(2 - 5 = -3\)
pet.cat-intercept:time.am-intercept cat minus mean when am, minus cat minus mean when pm, divided by 2 \(\frac{(Y_{ca} - Y_{.a}) - (Y_{cp} - Y_{.p})}{2}\) \(\frac{(0 - 2) - (6 - 8)}{2} = 0\) 
df %>%
  add_contrast("pet", "sum") %>%
  add_contrast("time", "sum") %>%
  lm(y ~ pet * time, .) %>%  
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 5 0.063 79.4 0
pet.cat-intercept -2 0.063 -31.8 0
time.am-intercept -3 0.063 -47.6 0
pet.cat-intercept:time.am-intercept 0 0.063 0.0 1
Difference
term interpretation formula value
intercept grand mean \(Y_{..}\) \(5\)
pet.dog-cat mean dog minus mean cat \(Y_{d.} - Y_{c.}\) \(7 - 3 = 4\)
time.pm-am mean pm minus mean am \(Y_{.p} - Y_{.a}\) \(8 - 2 = 6\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((10 - 6) - (4 - 0) = 0\) 
df %>%
  add_contrast("pet", "difference") %>%
  add_contrast("time", "difference") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 5 0.063 79.4 0
pet.dog-cat 4 0.126 31.8 0
time.pm-am 6 0.126 47.6 0
pet.dog-cat:time.pm-am 0 0.252 0.0 1
Helmert
term interpretation formula value
intercept grand mean \(Y_{..}\) \(5\)
pet.dog-cat mean dog minus mean cat \(Y_{d.} - Y_{c.}\) \(7 - 3 = 4\)
time.pm-am mean pm minus mean am \(Y_{.p} - Y_{.a}\) \(8 - 2 = 6\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((10 - 6) - (4 - 0) = 0\) 
df %>%
  add_contrast("pet", "helmert") %>%
  add_contrast("time", "helmert") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 5 0.063 79.4 0
pet.dog-cat 4 0.126 31.8 0
time.pm-am 6 0.126 47.6 0
pet.dog-cat:time.pm-am 0 0.252 0.0 1

N.B. In the case of 2-level factors, anova, difference, and Helmert coding are identical. Treatment coding differs only in the intercept.

Remember that interactions can always be described in two ways, since (A1 - A2) - (B1 - B2) == (A1 - B1) - (A2 - B2). Therefore, “dog minus cat when pm, minus dog minus cat when am” is the same as “pm minus am for dogs, minus pm minus am for cats”. The way you describe it in a paper depends on which version maps onto your hypothesis more straightforwardly. The examples above might be written as “the difference between dogs and cats was bigger in the evening than the morning” or “the difference between evening and morning was bigger for dogs than for cats”. Make sure you check the plots to make sure you are describing the relationships in the right direction.

2x3 Design

Let’s use simulated data with empirical = TRUE to explore how to interpret interactions between a 2-level factor and a 3-level factor coded in different ways.

mu <- c(0, 5, 7, 6, 2, 1)
df <- sim_design(between = list(time = c("am", "pm"),
                                pet = c("cat", "dog", "ferret")),
                 n = c(50, 60, 70, 80, 90, 100), mu = mu, empirical = TRUE)

cat dog ferret mean
am \(Y_{ca} = 0\) \(Y_{da} = 5\) \(Y_{fa} = 7\) \(Y_{.a} = 4\)
pm \(Y_{cp} = 6\) \(Y_{dp} = 2\) \(Y_{fp} = 1\) \(Y_{.p} = 3\)
mean \(Y_{c.} = 3\) \(Y_{d.} = 3.5\) \(Y_{f.} = 4\) \(Y_{..} = 3.5\)

Treatment
term interpretation formula value
intercept cat when am \(Y_{ca}\) \(0\)
pet.dog-cat dog minus cat, when am \(Y_{da} - Y_{ca}\) \(5 - 0 = 5\)
pet.ferret-cat ferret minus cat, when am \(Y_{fa} - Y_{ca}\) \(7 - 0 = 7\)
time.pm-am pm minus am, for cats \(Y_{cp} - Y_{ca}\) \(6 - 0 = 6\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((2 - 6) - (5 - 0) = -9\)
pet.ferret-cat:time.pm-am ferret minus cat when pm, minus ferret minus cat when am \((Y_{fp} - Y_{cp}) - (Y_{fa} - Y_{ca})\) \((1 - 6) - (7 - 0) = -12\) 
df %>%
  add_contrast("pet", "treatment") %>%
  add_contrast("time", "treatment") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 0 0.141 0.0 1
pet.dog-cat 5 0.191 26.1 0
pet.ferret-cat 7 0.185 37.8 0
time.pm-am 6 0.180 33.3 0
pet.dog-cat:time.pm-am -9 0.246 -36.7 0
pet.ferret-cat:time.pm-am -12 0.238 -50.4 0
Anova
term interpretation formula value
intercept grand mean \(Y_{..}\) \(3.5\)
pet.dog-cat mean dog minus mean cat \(Y_{d.} - Y_{c.}\) \(3.5 - 3 = 0.5\)
pet.ferret-cat mean ferret minus mean cat \(Y_{f.} - Y_{c.}\) \(4 - 3 = 1\)
time.pm-am mean pm minus mean am \(Y_{.p} - Y_{.a}\) \(3 - 4 = -1\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((2 - 6) - (5 - 0) = -9\)
pet.ferret-cat:time.pm-am ferret minus cat when pm, minus ferret minus cat when am \((Y_{fp} - Y_{cp}) - (Y_{fa} - Y_{ca})\) \((1 - 6) - (7 - 0) = -12\) 
df %>%
  add_contrast("pet", "anova") %>%
  add_contrast("time", "anova") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 3.5 0.048 72.22 0
pet.dog-cat 0.5 0.123 4.07 0
pet.ferret-cat 1.0 0.119 8.39 0
time.pm-am -1.0 0.097 -10.32 0
pet.dog-cat:time.pm-am -9.0 0.246 -36.66 0
pet.ferret-cat:time.pm-am -12.0 0.238 -50.36 0
Sum
term interpretation formula value
intercept grand mean \(Y_{..}\) \(3\)
pet.cat-intercept mean cat minus grand mean \(Y_{c.} - Y_{..}\) \(3 - 3.5 = -0.5\)
pet.dog-intercept mean dog minus grand mean \(Y_{d.} - Y_{..}\) \(3.5 - 3.5 = 0\)
time.am-intercept mean am minus grand mean \(Y_{.a} - Y_{..}\) \(4 - 3.5 = 0.5\)
pet.cat-intercept:time.am-intercept cat minus mean when am, minus cat minus mean when pm, divided by 2 \(\frac{(Y_{ca} - Y_{.a}) - (Y_{cp} - Y_{.p})}{2}\) \(\frac{(0 - 4) - (6 - 3)}{2} = -3.5\)
pet.dog-intercept:time.am-intercept dog minus mean when am, minus dog minus mean when pm, divided by 2 \(\frac{(Y_{da} - Y_{.a}) - (Y_{dp} - Y_{.p})}{2}\) \(\frac{(5 - 4) - (2 - 3)}{2} = 1\) 
df %>%
  add_contrast("pet", "sum") %>%
  add_contrast("time", "sum") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 3.5 0.048 72.22 0
pet.cat-intercept -0.5 0.071 -7.03 0
pet.dog-intercept 0.0 0.068 0.00 1
time.am-intercept 0.5 0.048 10.32 0
pet.cat-intercept:time.am-intercept -3.5 0.071 -49.22 0
pet.dog-intercept:time.am-intercept 1.0 0.068 14.64 0
Difference
term interpretation formula value
intercept grand mean \(Y_{..}\) \(3.5\)
pet.dog-cat mean dog minus mean cat \(Y_{d.} - Y_{c.}\) \(3.5 - 3 = 0.5\)
pet.ferret-dog mean ferret minus mean dog \(Y_{f.} - Y_{d.}\) \(4 - 3.5 = 0.5\)
time.pm-am mean pm minus mean am \(Y_{.p} - Y_{.a}\) \(3 - 4 = -1\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((2 - 6) - (5 - 0) = -9\)
pet.ferret-dog:time.pm-am ferret minus dog when pm, minus ferret minus dog when am \((Y_{fp} - Y_{dp}) - (Y_{fa} - Y_{da})\) \((1 - 2) - (7 - 5) = -3\) 
df %>%
  add_contrast("pet", "difference") %>%
  add_contrast("time", "difference") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 3.5 0.048 72.22 0
pet.dog-cat 0.5 0.123 4.07 0
pet.ferret-dog 0.5 0.114 4.38 0
time.pm-am -1.0 0.097 -10.32 0
pet.dog-cat:time.pm-am -9.0 0.246 -36.66 0
pet.ferret-dog:time.pm-am -3.0 0.228 -13.15 0
Helmert
term interpretation formula value
intercept grand mean \(Y_{..}\) \(3.5\)
pet.dog-cat mean dog minus mean cat \(Y_{d.} - Y_{c.}\) \(3.5 - 3 = 0.5\)
pet.ferret-cat.dog mean ferret minus mean of cat and dog \(Y_{f.} - \frac{Y_{c.} + Y_{d.}}{2}\) \(4 - \frac{3 + 3.5}{2} = 0.75\)
time.pm-am mean pm minus mean am \(Y_{.p} - Y_{.a}\) \(3 - 4 = -1\)
pet.dog-cat:time.pm-am dog minus cat when pm, minus dog minus cat when am \((Y_{dp} - Y_{cp}) - (Y_{da} - Y_{ca})\) \((2 - 6) - (5 - 0) = -9\)
pet.ferret-cat.dog:time.pm-am ferret minus mean of cat and dog when pm, minus ferret minus mean of cat and dog when am \((Y_{fp} - \frac{Y_{cp} + Y_{dp}}{2}) - (Y_{fa} - \frac{Y_{ca} + Y_{da}}{2})\) \((1 - \frac{6 + 2}{2}) - (7 - \frac{0 + 5}{2}) = -7.5\) 
df %>%
  add_contrast("pet", "helmert") %>%
  add_contrast("time", "helmert") %>%
  lm(y ~ pet * time, .) %>% 
  broom::tidy() %>% kable() %>% kable_styling()
term estimate std.error statistic p.value
(Intercept) 3.50 0.048 72.22 0
pet.dog-cat 0.50 0.123 4.07 0
pet.ferret-cat.dog 0.75 0.099 7.56 0
time.pm-am -1.00 0.097 -10.32 0
pet.dog-cat:time.pm-am -9.00 0.246 -36.66 0
pet.ferret-cat.dog:time.pm-am -7.50 0.198 -37.81 0

N.B. In this case, difference coding is identical to anova coding except that the second pet contrast is ferret versus dog instead of ferret versus cat.

3x3 Design

Please just don’t. You’re going to break my head.