sample()

First, let’s make a data frame with two variables, a and b that are both sampled from a normal distribution with a mean of 0 and SD of 1. The variablle n will be how many samples we’ll take (100). Then we can run a t-test to see if they are different.

library(tidyverse)

## ── Attaching packages ────────────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.2     ✓ purrr   0.3.4
## ✓ tibble  3.0.3     ✓ dplyr   1.0.2
## ✓ tidyr   1.1.1     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0

## ── Conflicts ───────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

n = 100

data <- data.frame(
  a = rnorm(n, 0, 1),
  b = rnorm(n, 0, 1)
)

t <- t.test(data$a,data$b)

t$p.value

## [1] 0.1527518

Now let’s repeat that procedure 1000 times. The easiest way to do that is to make a function that returns the information you want.

tPower <- function() {
  n = 100

  data <- data.frame(
    a = rnorm(n, 0, 1),
    b = rnorm(n, 0, 1)
  )

  t <- t.test(data$a,data$b)
  
  return(t$p.value)
}

tPower()

## [1] 0.7583175

mySample <- data.frame(
  p = replicate(10000, tPower())
) 

mySample %>%
  ggplot(aes(p)) +
  geom_histogram(bins = 20, boundary = 0)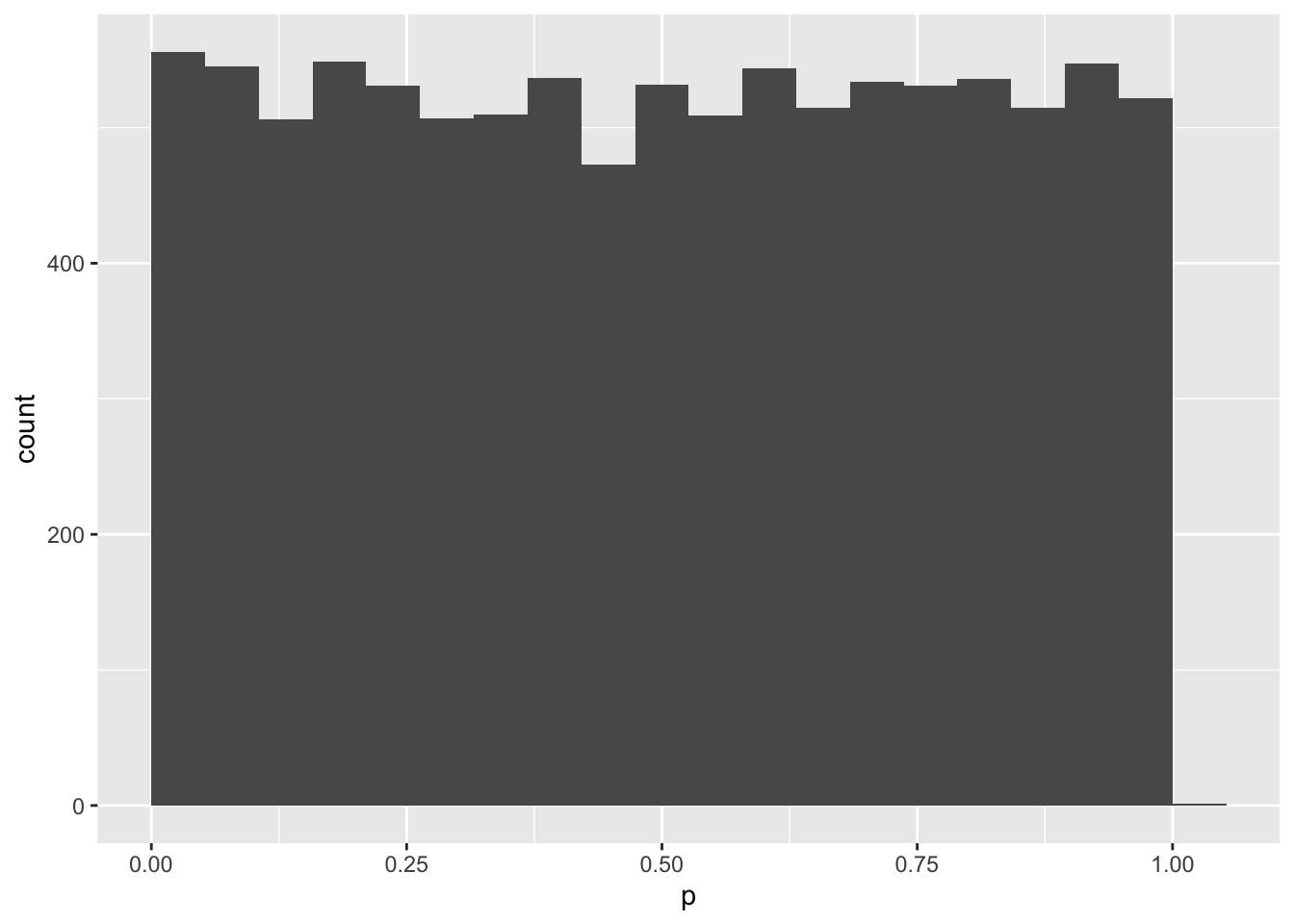

mean(mySample$p < .05)

## [1] 0.0528

What if you induced a small effect of 0.2 SD?

tPower2 <- function() {
  n = 100

  data <- data.frame(
    a = rnorm(n, 0, 1),
    b = rnorm(n, 0.2, 1)
  )

  t <- t.test(data$a,data$b)
  
  return(t$p.value)
}

tPower2()

## [1] 0.9142489

mySample2 <- data.frame(
  p = replicate(10000, tPower2())
) 

mySample2 %>%
  ggplot(aes(p)) +
  geom_histogram(bins = 20, boundary = 0)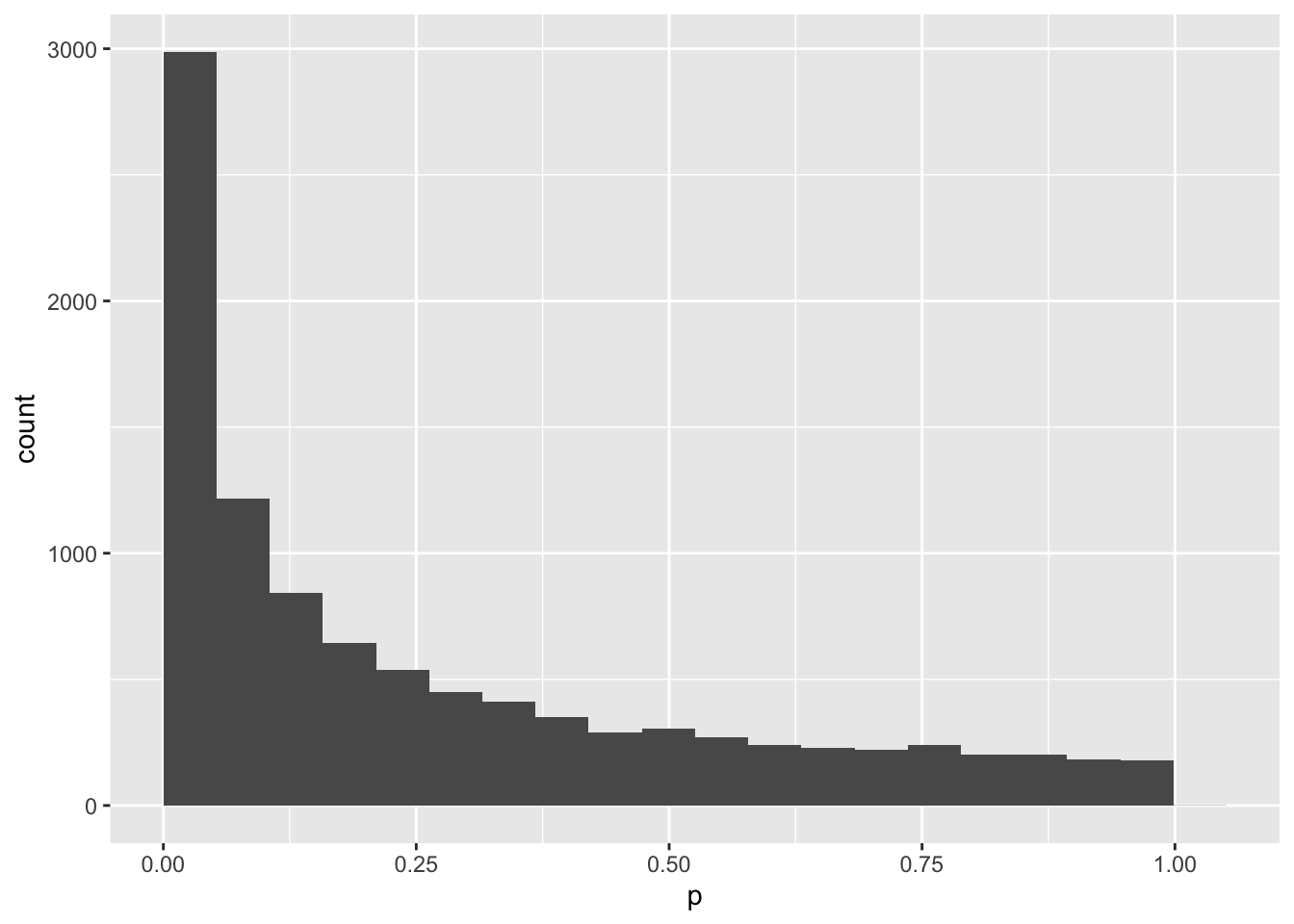

mean(mySample2$p < .05)

## [1] 0.2929

Hmm, you only get a p-value less than .05 30% of the time. That means that your study would only have 30% power to detect an effect this big with 100 subjects. Let’s make a new function to give you the p-value of a study with any number of subjects (you put the N inside the parentheses of the function).

tPowerN <- function(n) {

  data <- data.frame(
    a = rnorm(n, 0, 1),
    b = rnorm(n, 0.2, 1)
  )

  t <- t.test(data$a,data$b)
  
  return(t$p.value)
}

tPowerN(200)

## [1] 0.2969539

mySampleN <- data.frame(
  p200 = replicate(10000, tPowerN(200))
) 

mySampleN %>%
  ggplot(aes(p200)) +
  geom_histogram(bins = 20, boundary = 0)

mean(mySampleN$p200 < .05)

## [1] 0.5137

nlist <- seq(200, 1000, by = 100)

remove(mySampleN)
for (n in nlist) {
  temp <- data.frame(
    n = n,
    p = replicate(1000, tPowerN(n))
  ) 
  
  if (exists("mySampleN")) {
    mySampleN <- rbind(mySampleN, temp)
  } else {
    mySampleN <- temp
  }
  remove(temp)
  print(n)
}

## [1] 200
## [1] 300
## [1] 400
## [1] 500
## [1] 600
## [1] 700
## [1] 800
## [1] 900
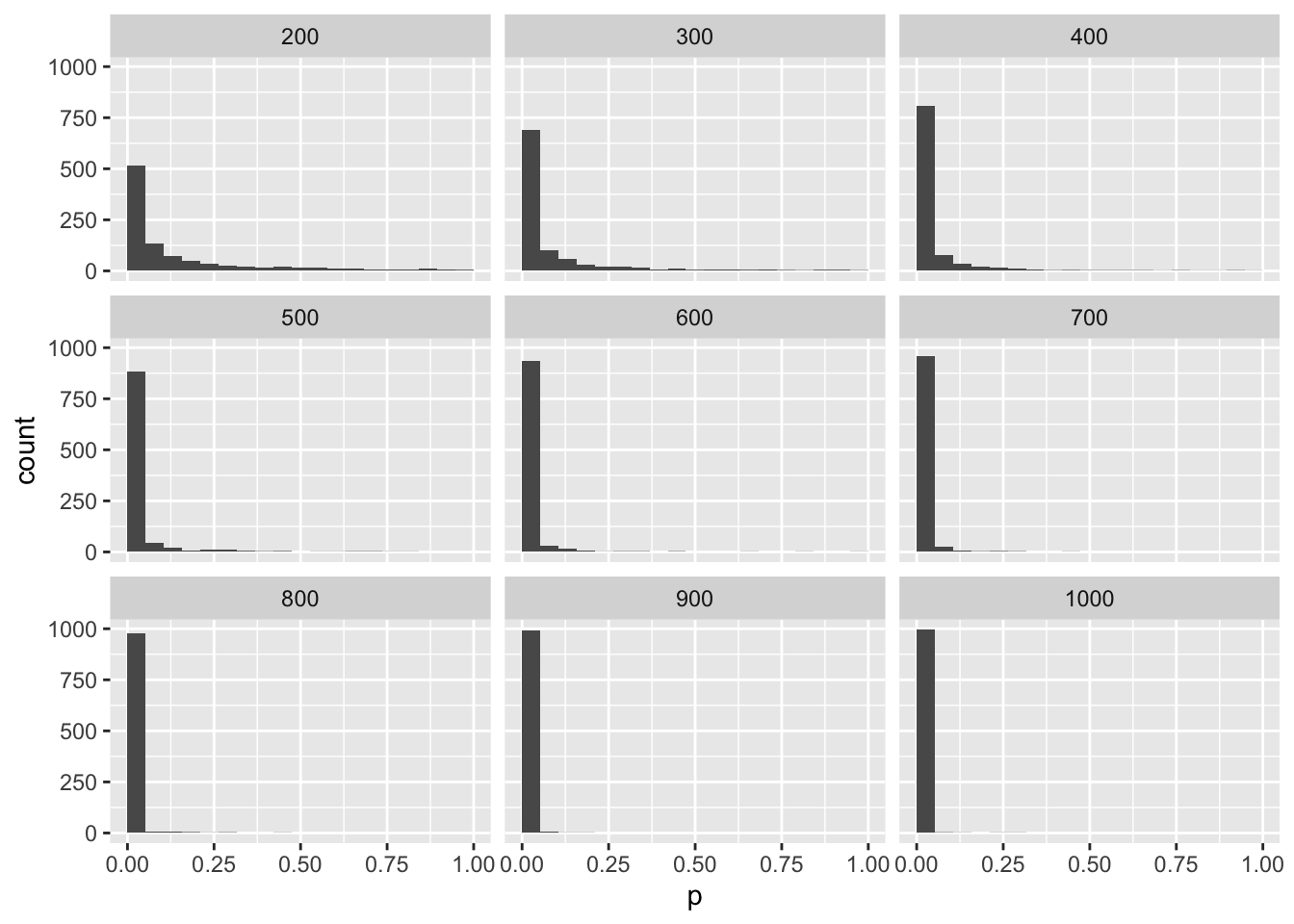
## [1] 1000

mySampleN %>%
  ggplot(aes(p)) +
  geom_histogram(bins = 20, boundary = 0) +
  facet_wrap(~n, nrow = 3)